
【题目】已知![]() 的顶点
的顶点![]() ,
, ![]() 边上的中线
边上的中线![]() 所在直线方程为
所在直线方程为![]() ,
, ![]() 边上的高
边上的高![]() 所在直线方程为
所在直线方程为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的方程.
的方程.
【答案】(1) C(5,3);(2) 6x-5y-15=0.
【解析】试题分析:(1)已知![]() 边上的高
边上的高![]() 所在直线方程,可得
所在直线方程,可得![]() 所在直线的斜率,联立
所在直线的斜率,联立![]() 和
和![]() 的直线方程即可求出点
的直线方程即可求出点![]() 的坐标(2)
的坐标(2)![]() 所在直线方程是
所在直线方程是![]() 边上的中线所在直线方程,则
边上的中线所在直线方程,则![]() 的中点坐标满足此直线方程,代入直线方程求得B 点所在直线方程联立直线方程求出B(0,-3),即可求出直线
的中点坐标满足此直线方程,代入直线方程求得B 点所在直线方程联立直线方程求出B(0,-3),即可求出直线![]() 的方程
的方程
解析:(1)依题意知:kAC=-2,A(6,1),
∴lAC为2x+y-13=0,
联立lAC、lCM得![]() ∴C(5,3).
∴C(5,3).
(2)设B(x0,y0),AB的中点M为(![]() ,
,![]() ),
),
代入2x-y-7=0,得2x0-y0-3=0,
∴![]() ∴B(0,-3),
∴B(0,-3),
∴kBC=![]() ,∴直线BC的方程为y=
,∴直线BC的方程为y=![]() x-3,
x-3,
即6x-5y-15=0.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |
(1)作出这些数据的频率分布直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);

(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次数学考试试题中共有![]() 道选择题,每道选择题都有
道选择题,每道选择题都有![]() 个选项,其中仅有一个是正确的.评分标准规定:“每题只选
个选项,其中仅有一个是正确的.评分标准规定:“每题只选![]() 项,答对得
项,答对得![]() 分,不答或答错得
分,不答或答错得![]() 分.”某考生每道题都给了一个答案,已确定有
分.”某考生每道题都给了一个答案,已确定有![]() 道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜,试求出该考生:
道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜,试求出该考生:
(Ⅰ)得![]() 分的概率;
分的概率;
(Ⅱ)所得分数![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数g(x)=f(x)+2x,x∈R为奇函数.
(1)判断函数f(x)的奇偶性;
(2)若x>0时,f(x)=log3x,求函数g(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,二次函数
中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
, ![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() .当
.当![]() 变化时,解答下列问题:
变化时,解答下列问题:
(1)以![]() 为直径的圆能否经过点
为直径的圆能否经过点![]() ?说明理由;
?说明理由;
(2)过![]() ,
, ![]() ,
, ![]() 三点的圆在
三点的圆在![]() 轴上截得的弦长是否为定值?若是,则求出该定值;若不是,请说明理由.
轴上截得的弦长是否为定值?若是,则求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,且
,且 ![]() .
.
(1)求m的值;
(2)判断f(x)在(0,+∞)上的单调性,并给予证明;
(3)求函数f(x)在区间[﹣5,﹣1]上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (
(![]() 为常数).
为常数).
(Ⅰ)求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)当函数![]() 在
在![]() 处取得极值
处取得极值![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(Ⅲ)当![]() 时,设
时,设![]() ,若函数
,若函数![]() 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设各项均为正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,且
,且![]() ,公比大于1的等比数列
,公比大于1的等比数列![]() 满足
满足![]() ,
, ![]() .
.
(1)求证数列![]() 是等差数列,并求其通项公式;
是等差数列,并求其通项公式;
(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)在(2)的条件下,若![]() 对一切正整数
对一切正整数![]() 恒成立,求实数
恒成立,求实数![]() 的取值
的取值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市积极倡导学生参与绿色环保活动,其中代号为“环保卫士—12369”的绿色环保活动小组对2014年1月—2014年12月(一年)内空气质量指数![]() 进行监测,下表是在这一年随机抽取的100天的统计结果:
进行监测,下表是在这一年随机抽取的100天的统计结果:
指数API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)若某市某企业每天由空气污染造成的经济损失![]() (单位:元)与空气质量指数
(单位:元)与空气质量指数![]() (记为
(记为![]() )的关系为:
)的关系为: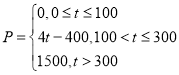 ,在这一年内随机抽取一天,估计该天经济损失
,在这一年内随机抽取一天,估计该天经济损失![]() 元的概率;
元的概率;
(2)若本次抽取的样本数据有30天是在供暖季节,其中有8天为重度污染,![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为某市本年度空气重度污染与供暖有关?
的把握认为某市本年度空气重度污染与供暖有关?
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季节 | |||
合计 | 100 |
下面临界值表供参考.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com