
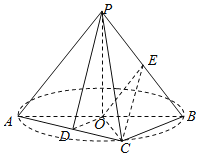
【题目】如图所示,底面![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() .
.

(1)设![]() 与
与![]() 交于点
交于点![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(2)求多面体![]() 的体积.
的体积.
 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:

(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的a,b的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高一实验班的数学成绩,采用抽样调查的方式,获取了![]() 位学生在第一学期末的数学成绩数据,样本统计结果如下表:
位学生在第一学期末的数学成绩数据,样本统计结果如下表:
分组 | 频数 | 频率 |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
合计 |
|
|
(1)求![]() 的值和实验班数学平均分的估计值;
的值和实验班数学平均分的估计值;
(2)如果用分层抽样的方法从数学成绩小于![]() 分的学生中抽取
分的学生中抽取![]() 名学生,再从这
名学生,再从这![]() 名学生中选
名学生中选![]() 人,求至少有一个学生的数学成绩是在
人,求至少有一个学生的数学成绩是在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,点C是圆上异于A、B的点,PO垂直于圆O所在的平面,且PO=OB![]() ,BC=2,点E在线段PB上,则CE+OE的最小值为_____.
,BC=2,点E在线段PB上,则CE+OE的最小值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PA=2,PA⊥平面ABCD,E是PC的中点,F是AB的中点.

(1)求证:BE∥平面PDF;
(2)求证:平面PDF⊥平面PAB;
(3)求BE与平面PAC所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,现以极点
,现以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的非负半轴建立平面直角坐标系,曲线
轴的非负半轴建立平面直角坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)若曲线![]() 为曲线
为曲线![]() 关于直线
关于直线![]() 的对称曲线,点
的对称曲线,点![]() 分别为曲线
分别为曲线![]() 、曲线
、曲线![]() 上的动点,点
上的动点,点![]() 坐标为
坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为![]() ,墙
,墙![]() 的长度为
的长度为![]() 米,(已有两面墙的可利用长度足够大),记
米,(已有两面墙的可利用长度足够大),记![]() .
.
(1)若![]() ,求
,求![]() 的周长(结果精确到0.01米);
的周长(结果精确到0.01米);
(2)为了使小动物能健康成长,要求所建的三角形露天活动室面积,![]() 的面积尽可能大,当
的面积尽可能大,当![]() 为何值时,该活动室面积最大?并求出最大面积.
为何值时,该活动室面积最大?并求出最大面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角![]() 中,
中,![]() , _______,求
, _______,求![]() 的周长
的周长![]() 的取值范围.
的取值范围.
①![]() ,
,![]() ,且
,且![]() ;
;
②![]() ;
;
③![]() ,
,![]() .
.
注:这三个条件中选一个,补充在上面的问题中并对其进行求解,如果选择多个条件分别解答,按第一个解答计分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com