
已知椭圆![]() 的中心为坐标原点
的中心为坐标原点![]() ,一个长轴端点为
,一个长轴端点为![]() ,短轴端点和焦点所组成的四边形为正方形,直线
,短轴端点和焦点所组成的四边形为正方形,直线![]() 与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且
与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且![]() .
.
(1)求椭圆方程;
(2)求m的取值范围.
(1)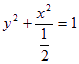 (2)所求m的取值范围为(-1,-
(2)所求m的取值范围为(-1,-![]() )∪(
)∪(![]() ,1)
,1)
【解题思路】通过![]() ,沟通A、B两点的坐标关系,再利用判别式和根与系数关系得到一个关于m的不等式。
,沟通A、B两点的坐标关系,再利用判别式和根与系数关系得到一个关于m的不等式。
(1)由题意可知椭圆![]() 为焦点在
为焦点在![]() 轴上的椭圆,可设
轴上的椭圆,可设![]()
由条件知![]() 且
且![]() ,又有
,又有![]() ,解得
,解得 ![]()
故椭圆![]() 的离心率为
的离心率为![]() ,其标准方程为:
,其标准方程为: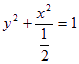
(2)设l与椭圆C交点为A(x1,y1),B(x2,y2)
得(k2+2)x2+2kmx+(m2-1)=0
Δ=(2km)2-4(k2+2)(m2-1)=4(k2-2m2+2)>0 (*)
x1+x2=, x1x2=
∵=3 ∴-x1=3x2 ∴
消去x2,得3(x1+x2)2+4x1x2=0,∴3()2+4=0
整理得4k2m2+2m2-k2-2=0
m2=时,上式不成立;m2≠时,k2=,
因λ=3 ∴k≠0 ∴k2=>0,∴-1<m<-![]() 或
或 ![]() <m<1
<m<1
容易验证k2>2m2-2成立,所以(*)成立
即所求m的取值范围为(-1,-![]() )∪(
)∪(![]() ,1)
,1)
【名师指引】椭圆与向量、解三角形的交汇问题是高考热点之一,应充分重视向量的功能


科目:高中数学 来源: 题型:
| OA |
| OB |
| a |
| OM |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a2 | c |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a2 | c |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com