
| A. | (0,1) | B. | (0,$\frac{1}{3}$] | C. | (0,$\frac{1}{6}$) | D. | ($\frac{1}{6}$,$\frac{1}{3}$] |
分析 通过讨论a的范围,结合函数的单调性问题转化为a<$\frac{x}{3}$在x∈[$\frac{1}{2}$,+∞)恒成立,求出a的范围即可.
解答 解:a>1时,f(x)递增,显然不满足$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<0,
0<a<1时,只需g(x)=x2-3ax>0在x∈[$\frac{1}{2}$,+∞)恒成立,
且g(x)在x∈[$\frac{1}{2}$,+∞)递增,
即a<$\frac{x}{3}$在x∈[$\frac{1}{2}$,+∞)恒成立且对称轴$\frac{3a}{2}$≤$\frac{1}{2}$,
故a<$\frac{1}{6}$,
故a的范围是(0,$\frac{1}{6}$),
故选:C.
点评 本题考查了函数的单调性、最值问题,考查对数函数的性质,是一道中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | d<0 | B. | S19<0 | ||
| C. | 当n=9时Sn取最小值 | D. | S10>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
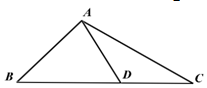 如图,在△ABC中,∠B=45°,D是BC边上一点,AB=$\frac{5}{2}\sqrt{6}$,AC=5$\sqrt{3}$,AD=5,∠ADB为锐角.
如图,在△ABC中,∠B=45°,D是BC边上一点,AB=$\frac{5}{2}\sqrt{6}$,AC=5$\sqrt{3}$,AD=5,∠ADB为锐角.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥α,m⊥n,则n∥α | B. | 若m∥α,n∥α,则m∥n | ||
| C. | 若m?β,且α⊥β,则m⊥α | D. | 若m⊥β,且α∥β,则m⊥α. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com