
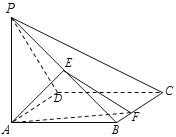
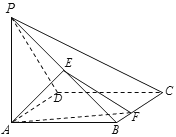
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 上的动点.
上的动点.
(1)平面![]() 与平面
与平面![]() 是否互相垂直?如果垂直,请证明;如果不垂直,请说明理由.
是否互相垂直?如果垂直,请证明;如果不垂直,请说明理由.
(2)若![]() ,
,![]() 为线段
为线段![]() 的三等分点,求多面体
的三等分点,求多面体![]() 的体积.
的体积.
【答案】(1)互相垂直,证明见解析(2)![]() 或
或![]() .
.
【解析】
(1)证明![]() 平面
平面![]() 中的
中的![]() 即可.
即可.
(2)利用多面体![]() 的体积为
的体积为![]() ,分
,分![]() 为线段
为线段![]() 的两个不同的三等分点进行求解即可.
的两个不同的三等分点进行求解即可.
解法一:(1)平面![]() 与平面
与平面![]() 互相垂直,
互相垂直,
理由如下:
因为![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() .
.
因为![]() 为正方形,所以
为正方形,所以![]()
又![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]()
因为![]() ,
,![]() 为线段
为线段![]() 的中点,所以
的中点,所以![]() ,
,
又![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)因为![]() 底面
底面![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,
所以点![]() 到底面
到底面![]() 的距离为
的距离为![]()
![]() ,
,
则![]() ,
,
又![]() 为线段
为线段![]() 的三等分点,
的三等分点,
当![]() 时,
时,![]() ,
,
所以多面体![]() 的体积为
的体积为![]() ;
;
当![]() 时,
时,![]() ,
,
所以多面体![]() 的体积为
的体积为![]() .
.
综上,多面体![]() 的体积为
的体积为![]() 或
或![]() .
.
解法二:(1)平面![]() 与平面
与平面![]() 互相垂直,
互相垂直,
理由如下:
因为![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,所以平面
,所以平面![]() 底面
底面![]() ,
,
又平面![]() 底面
底面![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]()
因为![]() ,
,![]() 为线段
为线段![]() 的中点,所以
的中点,所以![]() ,
,
又![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]()
(2)同解法一.


科目:高中数学 来源: 题型:
【题目】一种作图工具如图1所示.![]() 是滑槽
是滑槽![]() 的中点,短杆
的中点,短杆![]() 可绕
可绕![]() 转动,长杆
转动,长杆![]() 通过
通过![]() 处铰链与
处铰链与![]() 连接,
连接,![]() 上的栓子
上的栓子![]() 可沿滑槽AB滑动,且
可沿滑槽AB滑动,且![]() ,
,![]() .当栓子
.当栓子![]() 在滑槽AB内作往复运动时,带动
在滑槽AB内作往复运动时,带动![]() 绕
绕![]() 转动一周(
转动一周(![]() 不动时,
不动时,![]() 也不动),
也不动),![]() 处的笔尖画出的曲线记为
处的笔尖画出的曲线记为![]() .以
.以![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴建立如图2所示的平面直角坐标系.
轴建立如图2所示的平面直角坐标系.
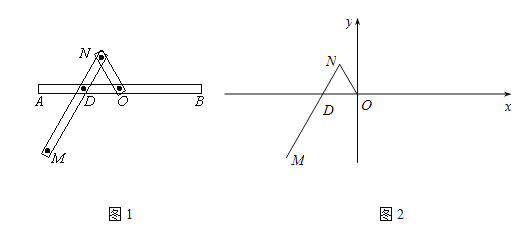
(Ⅰ)求曲线C的方程;
(Ⅱ)设动直线![]() 与两定直线
与两定直线![]() 和
和![]() 分别交于
分别交于![]() 两点.若直线
两点.若直线![]() 总与曲线
总与曲线![]() 有且只有一个公共点,试探究:
有且只有一个公共点,试探究:![]() 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
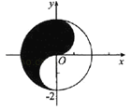
【题目】太极图被称为“中华第一图”.从孔庙大成殿梁柱,到楼观台、三茅宫标记物;从道袍、卦摊、中医、气功、武术到韩国国旗![]() ,太极图无不跃居其上.这种广为人知的太极图,其形状如阴阳两鱼互抱在一起,因而被称为“阴阳鱼太极图”.在如图所示的阴阳鱼图案中,阴影部分可表示为
,太极图无不跃居其上.这种广为人知的太极图,其形状如阴阳两鱼互抱在一起,因而被称为“阴阳鱼太极图”.在如图所示的阴阳鱼图案中,阴影部分可表示为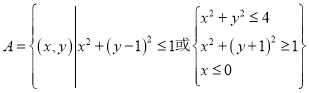 ,设点
,设点![]() ,则
,则![]() 的最大值与最小值之差是( )
的最大值与最小值之差是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租车公司给出的财务报表如下:
年度 项目 | 2014年 (1-12月) | 2015年 (1-12月) | 2016年 (1-11月) |
接单量(单) | 14463272 | 40125125 | 60331996 |
油费(元) | 214301962 | 581305364 | 653214963 |
平均每单油费 | 14.82 | 14.49 | |
平均每单里程 | 15 | 15 | |
每公里油耗 | 0.7 | 0.7 | 0.7 |
有投资者在研究上述报表时,发现租车公司有空驶情况,并给出空驶率的计算公式为![]() .
.
(1)分别计算2014,2015年该公司的空驶率的值(精确到0.01%);
(2)2016年该公司加强了流程管理,利用租车软件,降低了空驶率并提高了平均每单里程,核算截止到11月30日,空驶率在2015年的基础上降低了20个百分点,问2016年前11个月的平均每单油费和平均每单里程分别为多少?(分别精确到0.01元和0.01公里).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机调查了![]() 人,他们年龄的频数分布及支持“生育二胎”人数如下表:
人,他们年龄的频数分布及支持“生育二胎”人数如下表:
年龄 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
支持“生二胎” |
|
|
|
|
|
|
(1)由以上统计数据填下面![]() 列联表,并问是否有
列联表,并问是否有![]() 的把握认为以
的把握认为以![]() 岁为分界点对“生育二胎放开”政策的支持度有差异;
岁为分界点对“生育二胎放开”政策的支持度有差异;
年龄不低于 | 年龄低于 | 合计 | |
支持 |
|
| |
不支持 |
|
| |
合计 |
(2)若对年龄在![]() 的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司举办捐步公益活动,参与者通过捐赠每天的运动步数获得公司提供的牛奶,再将牛奶捐赠给留守儿童.此活动不但为公益事业作出了较大的贡献,公司还获得了相应的广告效益.据测算,首日参与活动人数为![]() 人,以后每天人数比前一天都增加
人,以后每天人数比前一天都增加![]() ,
,![]() 天后捐步人数稳定在第
天后捐步人数稳定在第![]() 天的水平,假设此项活动的启动资金为
天的水平,假设此项活动的启动资金为![]() 万元,每位捐步者每天可以使公司收益
万元,每位捐步者每天可以使公司收益![]() 元(以下人数精确到
元(以下人数精确到![]() 人,收益精确到
人,收益精确到![]() 元).
元).
(1)求活动开始后第![]() 天的捐步人数,及前
天的捐步人数,及前![]() 天公司的捐步总收益;
天公司的捐步总收益;
(2)活动开始第几天以后公司的捐步总收益可以收回启动资金并有盈余?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点是抛物线
的右焦点是抛物线![]()
![]() 的焦点,直线
的焦点,直线![]() 与
与![]() 相交于不同的两点
相交于不同的两点![]() .
.
(1)求![]() 的方程;
的方程;
(2)若直线![]() 经过点
经过点![]() ,求
,求![]() 的面积的最小值(
的面积的最小值(![]() 为坐标原点);
为坐标原点);
(3)已知点![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() 为线段
为线段![]() 的中点,求证:
的中点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种相互转化,相对统一的和谐美,定义:能够将圆![]() 的周长和面积同时等分成两个部分的函数称为圆
的周长和面积同时等分成两个部分的函数称为圆![]() 的一个“太极函数”,则下列有关说法中:
的一个“太极函数”,则下列有关说法中:

①对于圆![]() 的所有非常数函数的太极函数中,都不能为偶函数;
的所有非常数函数的太极函数中,都不能为偶函数;
②函数![]() 是圆
是圆![]() 的一个太极函数;
的一个太极函数;
③直线![]() 所对应的函数一定是圆
所对应的函数一定是圆![]() 的太极函数;
的太极函数;
④若函数![]() 是圆
是圆![]() 的太极函数,则
的太极函数,则![]()
所有正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,定义
,定义![]() ,
, ![]() .
.
(1) 若![]() ,是否存在
,是否存在![]() ,使得
,使得![]() ?请说明理由;
?请说明理由;
(2) 若![]() ,
, ![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3) 令![]() ,求证:“
,求证:“![]() 为等差数列”的充要条件是“
为等差数列”的充要条件是“![]() 的前4项为等差数列,且
的前4项为等差数列,且![]() 为等差数列”.
为等差数列”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com