
【题目】设![]() :实数
:实数![]() 满足
满足![]() ,其中
,其中![]() ;
; ![]() :实数
:实数![]() 满足
满足![]() .
.
(1)若![]() ,且
,且![]() 为真,求实数
为真,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]() 的必要不充分条件,求实数
的必要不充分条件,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 实数![]() 的取值范围是
的取值范围是![]() ;(2) 实数
;(2) 实数![]() 的取值范围是
的取值范围是![]() .
.
【解析】试题分析:(1)利用一元二次不等式的解法可化简命题p,q,若p∨q为真,则p,q至少有1个为真,即可得出;(2)根据p是q的必要不充分条件,即可得出.
试题解析:
(1)由x2﹣4ax+3a2<0,得(x﹣3a)(x﹣a)<0,
又a>0,所以a<x<3a,
当a=1时,1<x<3,即p为真时实数x的取值范围是1<x<3.
q为真时![]() 等价于(x﹣2)(x﹣3)<0,得2<x<3,
等价于(x﹣2)(x﹣3)<0,得2<x<3,
即q为真时实数x的取值范围是2<x<3.
若p∨q为真,则实数x的取值范围是1<x<3.
(2)p是q的必要不充分条件,等价于qp且p推不出q,
设A={x|a<x<3a},B={x|2<x<3},则BA;
则 ,
,
所以实数a的取值范围是1≤a≤2。


科目:高中数学 来源: 题型:
【题目】某食品厂定期购买面粉.已知该厂每天需用面粉6t,每吨面粉的价格为1800元,面粉的保管等其他费用为平均每吨每天3元,购面粉每次需支付运费900元.
(1)求该厂多少天购买一次面粉,才能使平均每天所支付的总费用最少?
(2)若提供面粉的公司规定:当一次购买面粉不少于210t时,其价格可享受9折优惠(即原价的90%),问该厂是否考虑利用此优惠条件?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在物理实验中,为了研究所挂物体的重量x对弹簧长度y的影响.某学生通过实验测量得到物体的重量与弹簧长度的对比表:
物体重量(单位g) | 1 | 2 | 3 | 4 | 5 |
弹簧长度(单位cm) | 1.5 | 3 | 4 | 5 | 6.5 |
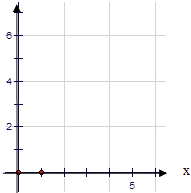
(1)画出散点图;
(2)利用公式(公式见卷首)求y对x的回归直线方程;
(3)预测所挂物体重量为8g时的弹簧长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家拟在2017年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() (单位:万件)与年促销费用
(单位:万件)与年促销费用![]() (单位:万元)(
(单位:万元)(![]() )满足
)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2017年该产品的利润![]() (单位:万元)表示为年促销费用
(单位:万元)表示为年促销费用![]() (单位:万元)的函数;
(单位:万元)的函数;
(2)该厂家2017年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
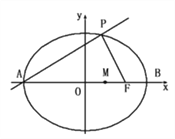
【题目】如图,A、B分别是椭圆![]() 的左、右端点,F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.
的左、右端点,F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.
(1)点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于MB,求椭圆上的点到点M的距离d的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1.
(Ⅰ)求数列{an}的通项公式.
(Ⅱ)设数列{bn}的前n项和为Tn,且Tn+![]() =λ(λ为常数),令cn=b2n(n∈N*).求数列{cn}的前n项和Rn.
=λ(λ为常数),令cn=b2n(n∈N*).求数列{cn}的前n项和Rn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线
轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线![]() 的参数方程是
的参数方程是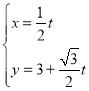 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,点
两点,点![]() 为
为![]() 的中点,点
的中点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 内,动点
内,动点![]() 与两定点
与两定点![]() ,
, ![]() 连线的斜率之积为
连线的斜率之积为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设点![]() ,
, ![]() 是轨迹
是轨迹![]() 上相异的两点.
上相异的两点.
(Ⅰ)过点![]() ,
, ![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() ,
, ![]() ,
, ![]() 与
与![]() 两条切线相交于点
两条切线相交于点![]() ,证明:
,证明: ![]() ;
;
(Ⅱ)若直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,证明:
,证明: ![]() 为定值,并求出这个定值.
为定值,并求出这个定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com