D
分析:设商贩购买甲、乙两种商品的件数分别为x、y,可赚钱z元,则z=x+1.8y,且满足4x+7y≤0,x、y≥0.因此,作出不等式组对应的平面区域,采用直线平移法并结合x、y都是整数,可算出购买甲、乙两种商品的件数分别为2件、6件时,可获最大利润12.8元.
解答:设商贩购买甲、乙两种商品的件数分别为x、y,可赚钱z元,
则z=x+1.8y,
其中x、y满足不等式组
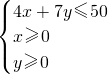
,
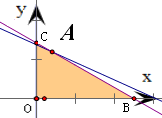
作出不等式组表示的平面区域,得到如图所示的△OBC及其内部
其中B(

,0),C(0,
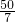
),O为坐标原点
设F(x,y)=z=x+1.8y,对应的直线为l,平移直线l使它经过区域内部
当l在y轴上的截距越大时,z的值越大
∵x∈N,y∈N,
∴当直线l经过区域内的点A(2,6)时,z达到最大值
因此z
max=F(2,6)=2+1.8×6=12.8元
即购买甲、乙两种商品的件数分别为2件、6件时,可获最大利润12.8元
故选:D
点评:本题给出实际应用问题,求利润最大时的成本分配.着重考查了二元一次不等式组对应的平面区域和运用线性规划知识解决实际应用问题的知识,属于中档题.

 则z=x+1.8y,
则z=x+1.8y,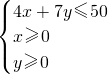 ,
, ,0),C(0,
,0),C(0,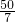 ),O为坐标原点
),O为坐标原点

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案