Question

已知函数f（x）=

1

3

x³+ax²+bx，且f′（-1）=0．
（1）试用含a的代数式表示b，并求f（x）的单调区间；
（2）令a=-1，设函数f（x）在x₁，x₂（x₁＜x₂）处取得极值，记点M （x₁，f（x₁）），N（x₂，f（x₂）），P（m，f（m）），x₁＜m＜x₂，请仔细观察曲线f（x）在点P处的切线与线段MP的位置变化趋势，并解释以下问题：
（Ⅰ）若对任意的t∈（x₁，x₂），线段MP与曲线f（x）均有异于M，P的公共点，试确定t的最小值，并证明你的结论；
（Ⅱ）若存在点Q（n，f（n）），x≤n＜m，使得线段PQ与曲线f（x）有异于P、Q的公共点，请直接写出m的取值范围（不必给出求解过程）．

Answer 1

分析：（1）欲求：“f（x）的单调区间”，对于三次函数而言，利用导数解决，本题还得对字母a进行讨论；
（2）存在性问题，结合观察f（x）的图象，帮助分析问题．

解答：解：（1）依题意，得f′（x）=x²+2ax+b，
由f′（-1）=1-2a+b=0得b=2a-1
从而f（x）=

1

3

x³+ax²+（2a-1）x，
故f′（x）=（x+1）（x+2a-1）
令f′（x）=0，得x=-1或x=1-2a
①当a＞1时，1-2a＜-1
当x变化时，根据f′（x）与f（x）的变化情况得，
函数f（x）的单调增区间为（-∞，1-2a）和（-1，+∞），单调减区间为（1-2a，-1）
②当a=1时，1-2a=-1，此时有f′（x）≥0恒成立，且仅在x=-1处f′（x）=0，故函数f（x）的单调增区间为R、
③当a＜1时，1-2a＞-1，同理可得，函数f（x）的单调增区间为（-∞，-1）和（1-2a，+∞），
单调减区间为（-1，1-2a）
综上：当a＞1时，函数f（x）的单调增区间为（-∞，1-2a）和（-1，+∞），单调减区间为（1-2a，-1）；
当a=1时，函数f（x）的单调增区间为R；
当a＜1时，函数f（x）的单调增区间为（-∞，-1）和（1-2a，+∞），单调减区间为（-1，1-2a）
（2）（Ⅰ）由a=-1得f（x）=

1

3

x³-x²-3x
令f′（x）=x²-2x-3=0得x₁=-1，x₂=3
由（1）得f（x）增区间为（-∞，-1）和（3，+∞），单调减区间为（-1，3），
所以函数f（x）在处x₁=-1，x₂=3处取得极值，故M（-1，

5

3

），N（3，-9）
观察f（x）的图象，有如下现象：

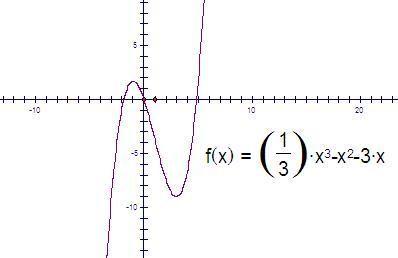
①当m从-1（不含-1）变化到3时，线段MP的斜率与曲线f（x）在点P处切线的斜率f（x）之差Kmp-f′（m）的值由正连续变为负、
②线段MP与曲线是否有异于H，P的公共点与Kmp-f′（m）的m正负有着密切的关联；
③Kmp-f′（m）=0对应的位置可能是临界点，故推测：满足Kmp-f′（m）的m就是所求的t最小值，下面给出证明并确定的t最小值、曲线f（x）在点P（m，f（m））处的切线斜率f′（m）=m²-2m-3；
线段MP的斜率Kmp=

m2-4m-5

3

，
当Kmp-f′（m）=0时，解得m=-1或m=2，
直线MP的方程为y=（

m2-4m-5

3

x+

m2- 4m

3

），
令g（x）=f（x）-（

m2-4m-5

3

x+

m2- 4m

3

），
当m=2时，g′（x）=x²-2x在（-1，2）上只有一个零点x=0，可判断f（x）函数在（-1，0）上单调递增，在（0，2）上单调递减，又g（-1）=g（2）=0，所以g（x）在（-1，2）上没有零点，即线段MP与曲线f（x）没有异于M，P的公共点、
当m∈（2，3]时，g（0）=-

m2-4m

3

＞0，
g（2）=-（m-2）²＜0，
所以存在δ∈（0，2]使得g（δ）=0，
即当m∈（2，3]时，MP与曲线f（x）有异于M，P的公共点
综上，t的最小值为2．
（Ⅱ）类似（1）于中的观察，可得m的取值范围为（1，3]．

点评：本题综合考查了函数导数的综合应用，本题是函数的综合题，综合考查了利用导数求函数的单调区间，求函数的极值，以及存在性问题，有一定的难度，是一道很好的压轴题．