
���� ��1��������ɵ�y=x+$\frac{1}{x}$�ĵ����Ժ�����㣬������ͼ��
��2��������ɵ�2b=16���ⷽ�̿ɵã�
��3���ɵ���������Сֵ�����f��1����f��2������������ۿɵã�
���  �⣺��1��������ɵ�y=x+$\frac{1}{x}$�ڣ�0��1�����Ǽ��������ڣ�1��+�ޣ�������������
�⣺��1��������ɵ�y=x+$\frac{1}{x}$�ڣ�0��1�����Ǽ��������ڣ�1��+�ޣ�������������
�ֺ���y=x+$\frac{1}{x}$Ϊ�溯�������ڣ�-1��0�����Ǽ��������ڣ�-�ޣ�-1��������������
�ҵ�x=1ʱy=2����x=-1ʱ��y=-2��������ͼ���£�
��2��������ɵ�2b=16�����b=4��
��3��������ɵ�f��x��=x+$\frac{c}{x}$�ڣ�0��$\sqrt{c}$�����Ǽ��������ڣ�$\sqrt{c}$��+�ޣ�������������
��c�ʣ�1��4������$\sqrt{c}$�ʣ�1��2�����ຯ���ڣ�1��$\sqrt{c}$�����Ǽ��������ڣ�$\sqrt{c}$��2��������������
�൱x=$\sqrt{c}$ʱ������ȡ��Сֵ$\sqrt{c}$+$\frac{4}{\sqrt{c}}$��f��1��=c+1��f��2��=2+$\frac{c}{2}$��
��c+1-��2+$\frac{c}{2}$��=$\frac{c}{2}$-1��0��2��c��4ʱ�����ֵΪf��1��=c+1��
��1��c��2ʱ�����ֵΪf��2��=2+$\frac{c}{2}$��
���� ���⿼�顰�Թ��������ĵ����ԣ����ν�ϲ�������֪��Ŀ�Ľ����ǽ������Ĺؼ������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ƽ�������һ����$\overrightarrow{a}$������$\overrightarrow{a}$=��$\overrightarrow{{e}_{1}}$+��$\overrightarrow{{e}_{2}}$���ˣ��̡�R�� | |
| B�� | ������ʵ����1����2��ʹ��1$\overrightarrow{{e}_{1}}$+��2$\overrightarrow{{e}_{2}}$=0�����1=��2=0 | |
| C�� | ��$\overrightarrow{{e}_{1}}$��$\overrightarrow{{e}_{2}}$�����ߣ���ռ���һ����$\overrightarrow{a}$������$\overrightarrow{a}$=��$\overrightarrow{{e}_{1}}$+��$\overrightarrow{{e}_{2}}$���ˣ��̡�R�� | |
| D�� | ��$\overrightarrow{{e}_{1}}$��$\overrightarrow{{e}_{2}}$�����ߣ���ƽ����һ����$\overrightarrow{a}$������$\overrightarrow{a}$=��$\overrightarrow{{e}_{1}}$+��$\overrightarrow{{e}_{2}}$���ˣ��̡�R�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\sqrt{3}$ | C�� | $\sqrt{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
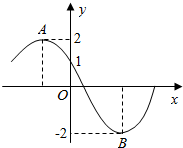 ��ͼΪ����f��x��=Msin����x+�գ���M��0���أ�0��0�ܦաܦУ��IJ���ͼ������A��B�ֱ�Ϊ����f��x������ߵ�����͵㣬��|AB|=5����ôf��-1��=��������
��ͼΪ����f��x��=Msin����x+�գ���M��0���أ�0��0�ܦաܦУ��IJ���ͼ������A��B�ֱ�Ϊ����f��x������ߵ�����͵㣬��|AB|=5����ôf��-1��=��������| A�� | 2 | B�� | $\sqrt{3}$ | C�� | -$\sqrt{3}$ | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | P��Q | B�� | P��Q | C�� | P��Q | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����y=f��x�����溯��������y=f��x����[0��5]�ϵ�ͼ������y=f��x����[-5��0���ϵ�ͼ��
��֪����y=f��x�����溯��������y=f��x����[0��5]�ϵ�ͼ������y=f��x����[-5��0���ϵ�ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ԲC1��x2+$\frac{{y}^{2}}{{b}^{2}}$=1��b��0�������Ҷ���ֱ�ΪA��B����PΪ˫����C2��x2-$\frac{{y}^{2}}{{b}^{2}}$=1�ڵ�һ�����ڵ�ͼ����һ�㣬ֱ��AP��BP����ԲC1�ֱ���C��D���㣮C��AP���е㣮
��ͼ����ԲC1��x2+$\frac{{y}^{2}}{{b}^{2}}$=1��b��0�������Ҷ���ֱ�ΪA��B����PΪ˫����C2��x2-$\frac{{y}^{2}}{{b}^{2}}$=1�ڵ�һ�����ڵ�ͼ����һ�㣬ֱ��AP��BP����ԲC1�ֱ���C��D���㣮C��AP���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com