
【题目】已知抛物线![]() 的焦点为
的焦点为![]() .
.
(1)若抛物线![]() 的焦点到准线的距离为4,直线
的焦点到准线的距离为4,直线![]() ,求直线
,求直线![]() 截抛物线
截抛物线![]() 所得的弦长;
所得的弦长;
(2)过点![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,过点
两点,过点![]() 作抛物线的切线,两切线相交于点
作抛物线的切线,两切线相交于点![]() ,若
,若![]() 分别表示直线
分别表示直线![]() 与直线
与直线![]() 的斜率,且
的斜率,且![]() ,求
,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的顶点在坐标原点,焦点在x轴上,且过点(2,4),圆
的顶点在坐标原点,焦点在x轴上,且过点(2,4),圆![]() ,过圆心
,过圆心![]() 的直线l与抛物线和圆分别交于P,Q,M,N,则
的直线l与抛物线和圆分别交于P,Q,M,N,则![]() 的最小值为________.
的最小值为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在圆![]() 内有一点
内有一点![]() ,
,![]() 为圆
为圆![]() 上一动点,线段
上一动点,线段![]() 的垂直平分线与
的垂直平分线与![]() 的连线交于点
的连线交于点![]() .
.
(Ⅰ)求点![]() 的轨迹方程.
的轨迹方程.
(Ⅱ)若动直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 、
、![]() 两点,且以
两点,且以![]() 为直径的圆恒过坐标原点
为直径的圆恒过坐标原点![]() .问是否存在一个定圆与动直线
.问是否存在一个定圆与动直线![]() 总相切.若存在,求出该定圆的方程;若不存在,请说明理由.
总相切.若存在,求出该定圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中华民族是一个传统文化丰富多彩的民族,各民族有许多优良的传统习俗,如过大年吃饺子,元宵节吃汤圆,端午节吃粽子,中秋节吃月饼等等,让人们感受到浓浓的节目味道,某家庭过大年时包有大小和外观完全相同的肉馅饺子、蛋馅饺子和素馅饺子,一家4口人围坐在桌旁吃年夜饭,当晚该家庭吃饺子时每盘中混放8个饺子,其中肉馅饺子4个,蛋馅饺子和素馅饺子各2个,若在桌上上一盘饺子大家共同吃,记每个人第1次夹起的饺子中肉馅饺子的个数为![]() ,若每个人各上一盘饺子,记4个人中第1次夹起的是肉馅饺子的人数为
,若每个人各上一盘饺子,记4个人中第1次夹起的是肉馅饺子的人数为![]() ,假设每个人都吃饺子,且每人每次都是随机地从盘中夹起饺子.
,假设每个人都吃饺子,且每人每次都是随机地从盘中夹起饺子.
(1)求随机变量![]() 的分布列;
的分布列;
(2)若![]() 的数学期望分别记为
的数学期望分别记为![]() 、
、![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 且
且![]() .
.
(1)求实数![]() 的值;
的值;
(2)判断函数![]() 在区间
在区间![]() 上的单调性,并用函数单调性的定义证明;
上的单调性,并用函数单调性的定义证明;
(3)求实数![]() 的取值范围,使得关于
的取值范围,使得关于![]() 的方程
的方程![]() 分别为:
分别为:
①有且仅有一个实数解;②有两个不同的实数解;③有三个不同的实数解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 与
与![]() 分别是边长为1与2的正三角形,
分别是边长为1与2的正三角形, ![]() ,四边形
,四边形![]() 为直角梯形,且
为直角梯形,且![]() ,
, ![]() ,点
,点![]() 为
为![]() 的重心,
的重心, ![]() 为
为![]() 中点,
中点, ![]() 平面
平面![]() ,
, ![]() 为线段
为线段![]() 上靠近点
上靠近点![]() 的三等分点.
的三等分点.
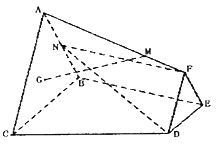
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)若二面角![]() 的余弦值为
的余弦值为![]() ,试求异面直线
,试求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com