
【题目】定义域为![]() 的偶函数
的偶函数![]() 满足对
满足对![]() ,有
,有![]() ,且当
,且当![]() 时,
时, ![]() ,若函数
,若函数![]() 在
在![]() 上至多有三个零点,则
上至多有三个零点,则![]() 的取值范围是
的取值范围是
__________.
【答案】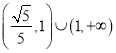
【解析】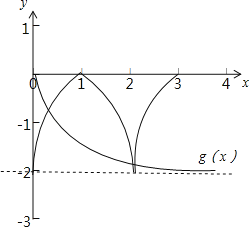
∵f(x+2)=f(x)﹣f(1),
且f(x)是定义域为R的偶函数,
令x=﹣1可得f(﹣1+2)=f(﹣1)﹣f(1),
又f(﹣1)=f(1),
∴f(1)=0 则有f(x+2)=f(x),
∴f(x)是最小正周期为2的偶函数.
当x∈[2,3]时,f(x)=﹣2x2+12x﹣18=﹣2(x﹣3)2,
函数的图象为开口向下、顶点为(3,0)的抛物线.
∵函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至少有三个零点,
令g(x)=loga(|x|+1),则f(x)的图象和g(x)的图象至多有3个交点.
可以分两种情况:其一是有交点时,其二是一个交点也没有,
当一个交点都没有时,即a>1.
当有交点时,∵f(x)≤0,∴g(x)≤0,可得0<a<1,
要使函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至多有三个零点,
则有g(4)<f(4),可得 loga(4+1)>f(4)=﹣2,
即loga5<﹣2,∴5>![]() ,解得,又0<a<1,∴
,解得,又0<a<1,∴![]() <a<1,
<a<1,
故答案为: 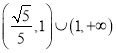 。
。


科目:高中数学 来源: 题型:
【题目】袋中有大小相同的3个红球和2个白球,现从袋中每次取出一个球,若取出的是红球,则放回袋中,继续取一个球,若取出的是白球,则不放回,再从袋中取一球,直到取出两个白球或者取球5次,则停止取球,设取球次数为![]() ,
,
(1)求取球3次则停止取球的概率;
(2)求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() (
(![]() )与直线
)与直线![]() :
:![]() 相切,设点
相切,设点![]() 为圆上一动点,
为圆上一动点,![]() 轴于
轴于![]() ,且动点
,且动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)直线![]() 与直线
与直线![]() 垂直且与曲线
垂直且与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对人们休闲方式的一次调查中,共调查120人,其中女性70人,男性50人.女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外30人主要的休闲方式是运动.
(1)根据以上数据建立一个2×的列联表:
休闲方式 性别 | 看电视 | 运 动 | 总 计 |
女 性 | |||
男 性 | |||
总 计 |
(2)有多大的把握认为休闲方式与性别有关?
参考公式及数据:K2=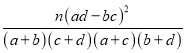
①当K2>2.706时,有90%的把握认为A、B有关联;
②当K2>3.841时,有95%的把握认为A、B有关联;
③当K2>6.635时,有99%的把握认为A、B有关联.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级共有1000名学生,其中男生650人,女生350人,为了调查学生周末的休闲方式,用分层抽样的方法抽查了200名学生.
(Ⅰ)完成下面的![]() 列联表;
列联表;
不喜欢运动 | 喜欢运动 | 合计 | |
女生 | 50 | ||
男生 | |||
合计 | 100 | 200 |
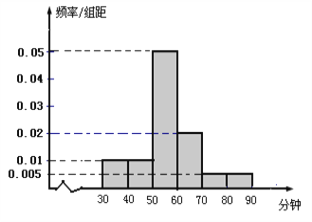
(Ⅱ)在抽取的样本中,调查喜欢运动女生的运动时间,发现她们的运动时间介于30分钟到90分钟之间,右图是测量结果的频率分布直方图,若从区间段![]() 和
和![]() 的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.
的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用C(A)表示非空集合A中的元素个数,定义A*B=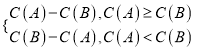 若A={1,2},B={x|(x2+ax)·(x2+ax+2)=0},且A*B=1,设实数a的所有可能取值组成的集合是S,则C(S)等于( )
若A={1,2},B={x|(x2+ax)·(x2+ax+2)=0},且A*B=1,设实数a的所有可能取值组成的集合是S,则C(S)等于( )
A. 1 B. 3
C. 5 D. 7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)将曲线![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角
的倾斜角![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某购物网站对在7座城市的线下体验店的广告费指出![]() (万元)和销售额
(万元)和销售额![]() (万元)的数据统计如下表:
(万元)的数据统计如下表:
城市 |
|
|
|
|
|
|
|
广告费支出 |
|
|
|
|
|
|
|
销售额 |
|
|
|
|
|
|
|
(Ⅰ)若用线性回归模型拟合![]() 与
与![]() 关系,求
关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)若用对数函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程
的关系,可得回归方程![]() ,经计算对数函数回归模型的相关系数约为
,经计算对数函数回归模型的相关系数约为![]() ,请说明选择哪个回归模型更合适,并用此模型预测
,请说明选择哪个回归模型更合适,并用此模型预测![]() 城市的广告费用支出
城市的广告费用支出![]() 万元时的销售额.
万元时的销售额.
参考数据: ![]() ,
, ![]() ,
, ![]() ,
, 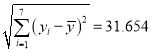 ,
, ![]() ,
, ![]() .
.
参考公式: 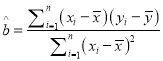 ,
, ![]() .
.
相关系数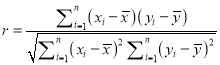 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com