
分析 (1)走路线①20分钟到校,意味着张老师在A、B处均遇到绿灯,由此能求出张老师选择路线①,他20分钟能到校的概率.
(2)设选择khxg①延误时间为随机变量ξ,则ξ的所有可能取值为0,2,3,5,分别求出相应的概率,从而求出Eξ=2;设选择路线②延误时间为随机变量η,则η的可能取值为0,8,5,13,分别求出相应的概率,从而求出Eη=5.由此求出为使张老师日常上班途中所花时间较少,建议张老师选择路线②.
解答 解:(1)走路线①20分钟到校,意味着张老师在A、B处均遇到绿灯,
∴张老师选择路线①,他20分钟能到校的概率p=$\frac{1}{2}×\frac{2}{3}$=$\frac{1}{3}$.
(2)设选择khxg①延误时间为随机变量ξ,则ξ的所有可能取值为0,2,3,5,
则P(ξ=0)=$\frac{1}{2}×\frac{2}{3}=\frac{1}{3}$,
P(ξ=2)=$\frac{1}{2}×\frac{2}{3}=\frac{1}{3}$,
P(ξ=3)=$\frac{1}{2}×\frac{1}{3}=\frac{1}{6}$,
P(ξ=4)=$\frac{1}{2}×\frac{1}{3}=\frac{1}{6}$,
Eξ=$0×\frac{1}{3}+2×\frac{1}{3}+3×\frac{1}{6}+5×\frac{1}{6}=2$.
设选择路线②延误时间为随机变量η,则η的可能取值为0,8,5,13,
P(η=0)=$\frac{3}{4}×\frac{2}{5}=\frac{6}{20}$,
P(η=8)=$\frac{1}{4}×\frac{2}{5}=\frac{2}{20}$,
P(η=5)=$\frac{3}{4}×\frac{3}{5}$=$\frac{9}{20}$,
P(η=13)=$\frac{1}{4}×\frac{3}{5}=\frac{3}{20}$,
Eη=$0×\frac{6}{20}+8×\frac{2}{20}+5×\frac{9}{20}+13×\frac{3}{20}$=5.
∴选择路线①平均所花时间为20+2=22分钟;选择路线②平均所花时间为15+5=20分钟.
∴为使张老师日常上班途中所花时间较少,建议张老师选择路线②.
点评 本题考查概率的求法,考查离散型随机变量的数学期望的求法及应用,是中档题,解题时要认真审题,注意相互独立事件概率乘法公式的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
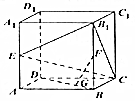 如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB.
如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com