
【题目】若两个函数的图象经过若干次平移后能够重合,则称这两个函数为“同形”函数,给出下列四个函数:![]() ,
,![]() ,
,![]() ,
,![]() ,则“同形”函数是( )
,则“同形”函数是( )
A.![]() 与
与![]() B.
B.![]() 与
与![]() C.
C.![]() 与
与![]() D.
D.![]() 与
与![]()
科目:高中数学 来源: 题型:
【题目】如图,A、B是海岸线OM、ON上两个码头,海中小岛有码头Q到海岸线OM、ON的距离分别为![]() 、
、![]() ,测得
,测得![]() ,
,![]() ,以点O为坐标原点,射线OM为x轴的正半轴,建立如图所示的直角坐标系,一艘游轮以
,以点O为坐标原点,射线OM为x轴的正半轴,建立如图所示的直角坐标系,一艘游轮以![]() 小时的平均速度在水上旅游线AB航行(将航线AB看作直线,码头Q在第一象限,航线BB经过点Q).
小时的平均速度在水上旅游线AB航行(将航线AB看作直线,码头Q在第一象限,航线BB经过点Q).
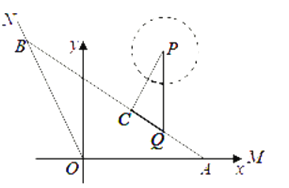
(1)问游轮自码头A沿![]() 方向开往码头B共需多少分钟?
方向开往码头B共需多少分钟?
(2)海中有一处景点P(设点P在![]() 平面内,
平面内,![]() ,且
,且![]() ),游轮无法靠近,求游轮在水上旅游线AB航行时离景点P最近的点C的坐标.
),游轮无法靠近,求游轮在水上旅游线AB航行时离景点P最近的点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的焦距为
)的焦距为![]() ,且右焦点F与短轴的两个端点组成一个正三角形.若直线l与椭圆C交于
,且右焦点F与短轴的两个端点组成一个正三角形.若直线l与椭圆C交于![]() 、
、![]() ,且在椭圆C上存在点M,使得:
,且在椭圆C上存在点M,使得:![]() (其中O为坐标原点),则称直线l具有性质H.
(其中O为坐标原点),则称直线l具有性质H.
(1)求椭圆C的方程;
(2)若直线l垂直于x轴,且具有性质H,求直线l的方程;
(3)求证:在椭圆C上不存在三个不同的点P、Q、R,使得直线![]() 、
、![]() 、
、![]() 都具有性质H.
都具有性质H.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】福彩是利国利民游戏,其刮刮乐之《蓝色奇迹》:如图(1)示例,刮开票面看到最左侧一列四个两位数字为“我的号码”,最上行四个两位数为“中奖号码”,这八个两位数是00至99这一百个数字随机产生的,若两个数字相同即中得其相交线上的奖金,奖金可以累加.小明买的一张《蓝色奇迹》刮刮乐如图(2),除了一个“我的号码”外,他已经刮开票面上其它所有数字,依据目前的信息,小明从这张刮刮乐得到的奖金额高于600元的概率为(无所得税)( )


图(1) 图(2)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知曲线![]() 的方程为
的方程为![]() ,曲线
,曲线![]() 的方程为
的方程为![]() .以极点
.以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴正半轴建立直角坐标系
轴正半轴建立直角坐标系![]() .
.
(1)求曲线![]() ,
,![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与曲线
,与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() ,抛物线
,抛物线![]() 的焦点F是椭圆
的焦点F是椭圆![]() 的顶点.
的顶点.
(1)求![]() 与
与![]() 的标准方程;
的标准方程;
(2)![]() 上不同于F的两点P,Q满足以PQ为直径的圆经过F,且直线PQ与
上不同于F的两点P,Q满足以PQ为直径的圆经过F,且直线PQ与![]() 相切,求
相切,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,当P(x,y)不是原点时,定义P的“伴随点”为![]() ;
;
当P是原点时,定义P的“伴随点“为它自身,平面曲线C上所有点的“伴随点”所构成的曲线![]() 定义为曲线C的“伴随曲线”.现有下列命题:
定义为曲线C的“伴随曲线”.现有下列命题:
①若点A的“伴随点”是点![]() ,则点
,则点![]() 的“伴随点”是点A
的“伴随点”是点A
②单位圆的“伴随曲线”是它自身;
③若曲线C关于x轴对称,则其“伴随曲线”![]() 关于y轴对称;
关于y轴对称;
④一条直线的“伴随曲线”是一条直线.
其中的真命题是_____________(写出所有真命题的序列).
查看答案和解析>>
科目:高中数学 来源: 题型:
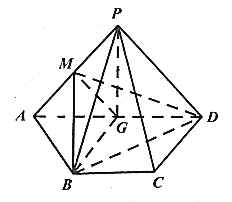
【题目】如图,已知四边形![]() 的直角梯形,
的直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 平面
平面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点(
上一点(![]() 不与端点重合).
不与端点重合).
(Ⅰ)若![]() ,
,
(i)求证:![]() 平面
平面![]() ;
;
(ii)求直线![]() 与平面
与平面![]() 所成的角的大小;
所成的角的大小;
(Ⅱ)否存在实数![]() 满足
满足![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成的锐角为
所成的锐角为![]() ,若存在,确定
,若存在,确定![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com