
【题目】已知向量 ![]() =(cosx,﹣1),
=(cosx,﹣1), ![]() =(
=( ![]() sinx,cos2x),设函数f(x)=
sinx,cos2x),设函数f(x)= ![]()
![]() +
+ ![]() .
.
(Ⅰ)求函数f(x)的最小正周期和单调递增区间;
(Ⅱ)当x∈(0, ![]() )时,求函数f(x)的值域.
)时,求函数f(x)的值域.
科目:高中数学 来源: 题型:
【题目】大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至11月份销售某种机械配件的销售量及销售单价进行了调查,销售单价x元和销售量y件之间的一组数据如表所示:
月份 | 7 | 8 | 9 | 10 | 11 |
销售单价x元 | 9 | 9.5 | 10 | 10.5 | 11 |
销售量y件 | 11 | 10 | 8 | 6 | 5 |
(1)根据7至11月份的数据,求出y关于x的回归直线方程;
(2)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润? 参考公式:回归直线方程 ![]() =b
=b ![]() +a,其中b=
+a,其中b= 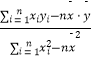 .
.
参考数据: ![]() =392,
=392, ![]() =502.5.
=502.5.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正三角形ABC的边长为2,AM是边BC上的高,沿AM将△ABM折起,使得二面角B﹣AM﹣C的大小为90°,此时点M到平面ABC的距离为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是市儿童乐园里一块平行四边形草地ABCD,乐园管理处准备过线段AB上一点E设计一条直线EF(点F在边BC或CD上,不计路的宽度),将该草地分为面积之比为2:1的左、右两部分,分别种植不同的花卉.经测量得AB=18m,BC=10m,∠ABC=120°.设EB=x,EF=y(单位:m). 
(1)当点F与C重合时,试确定点E的位置;
(2)求y关于x的函数关系式;
(3)请确定点E、F的位置,使直路EF长度最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个样本M的数据是x1 , x2 , ,xn , 它的平均数是5,另一个样本N的数据x12 , x22 , ,xn2它的平均数是34.那么下面的结果一定正确的是( )
A.SM2=9
B.SN2=9
C.SM2=3
D.Sn2=3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学有刘徽发现当圆内接多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的“徽率”.某同学利用刘徽的“割圆术”思想设计了一个计算圆周率的近似值的程序框图如图,则输出S的值为 (参考数据:sin15°=0.2588,sin7.5°=0.1305)( )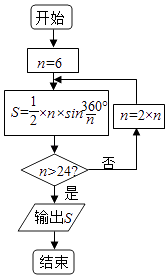
A.2.598
B.3.106
C.3.132
D.3.142
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图: 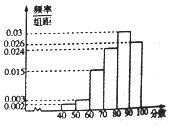
(I)为了了解部分市民对“共享单车”评分较低的原因,该部门从评分低于60分的市民中随机抽取2人进行座谈,求这2人评分恰好都在[50,60)的概率;
(II)根据你所学的统计知识,判断该项目能否通过考核,并说明理由.
(注:满意指数= ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com