
分析 (1)令2x+5=t,换元可得y=-$\frac{1}{2}$+$\frac{7}{2t}$,由$\frac{7}{2t}$≠0可得;
(2)令s=x2+x+2=(x+$\frac{1}{2}$)2+$\frac{7}{4}$≥$\frac{7}{4}$,换元由不等式的性质可得.
解答 解:(1)令2x+5=t,则x=$\frac{1}{2}$(t-5),
∴y=$\frac{1-x}{2x+5}$=$\frac{1-\frac{1}{2}(t-5)}{t}$=-$\frac{1}{2}$+$\frac{7}{2t}$,
∵$\frac{7}{2t}$≠0,∴-$\frac{1}{2}$+$\frac{7}{2t}$≠-$\frac{1}{2}$,
故函数的值域为{x|x≠-$\frac{1}{2}$};
(2)令s=x2+x+2=(x+$\frac{1}{2}$)2+$\frac{7}{4}$≥$\frac{7}{4}$,
∴y=$\frac{{x}^{2}+x+1}{{x}^{2}+x+2}$=$\frac{s-1}{s}$=1-$\frac{1}{s}$,
∵s≥$\frac{7}{4}$,∴0<$\frac{1}{s}$≤$\frac{4}{7}$,
∴-$\frac{4}{7}$≤-$\frac{1}{s}$<0,∴$\frac{3}{7}$≤1-$\frac{1}{s}$<1,
∴函数的值域为[$\frac{3}{7}$,1)
点评 本题考查函数的值域,涉及换元法和不等式的性质,属基础题.


科目:高中数学 来源: 题型:填空题
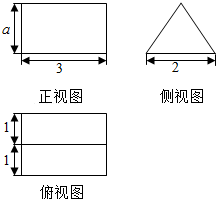 如图是一个几何体的三视图,若它的体积是3$\sqrt{3}$,则a=$\sqrt{3}$,该几何体的表面积为2$\sqrt{3}$+18.
如图是一个几何体的三视图,若它的体积是3$\sqrt{3}$,则a=$\sqrt{3}$,该几何体的表面积为2$\sqrt{3}$+18.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com