
(本题满分12分)
为调查某工厂工人生产某种产品的能力,随机抽查了一些工人某天生产产品的数量,产品数量的分组区间为[45,55), [55,65), [65,75), [75,85), [85,95),由此得到频率分布直方图如图所示,保存中不慎丢失一些数据,但已知第一组 ([45,55) ]有4人;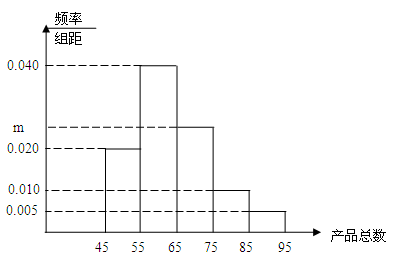
(Ⅰ)求被抽查的工人总人数n及图中所示m为多少;
(Ⅱ)求这些工人中一天生产该产品数量在[55,75)之间的人数是多少。
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:解答题
由于当前学生课业负担较重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,
小数点后的一位数字为叶)如图示:
| | |
| 4 | 3 5 6 6 6 7 7 7 8 8 9 9 |
| 5 | 0 1 1 2 |
 表示抽到“健康视力”学生的人数,求
表示抽到“健康视力”学生的人数,求 的分布列及数学期望
的分布列及数学期望查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示。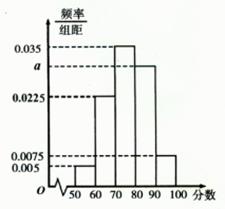
(1)请根据图中所给数据,求出 的值;
的值;
(2)从成绩在[50,70)内的学生中随机选3名学生,求这3名学生的成绩都在[60,70)内的概率;
(3)为了了解学生本次考试的失分情况,从成绩在[50,70)内的学生中随机选取3人的成绩进行分析,用X表示所选学生成绩在[ 60,70)内的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80 mg/100ml(不含80)之间,属于酒后驾车;在80mg/100ml(含80)以上时,属醉酒驾车,对于酒后驾车和醉酒驾车的驾驶员公安机关将给予不同程度的处罚.
某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后
驾车和醉酒驾车的驾驶员20人,下图是对这20人血液中酒精含量进行检查所得结果的频率分布
直方图.
(1)根据频率分布直方图,求此次抽查的250人中,醉酒驾车的人数;
(2)从血液酒精浓度在[70,90)范围内的驾驶员中任取2人,求恰有1人属于醉酒驾车的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解目前老年人居家养老还是在敬老院养老的意向,共调查了50名老年人,其中男性明确表示去敬老院养老的有5人,女性明确表示居家养老的有10人,已知在全部50人中随机地抽取1人明确表示居家养老的概率为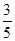 。
。
(1)请根据上述数据建立一个2×2列联表;
(2)居家养老是否与性别有关?请说明理由。
参考公式: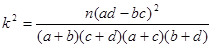
参考数据:
 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
以下是某地搜集到的新房屋的销售价格 和房屋的面积
和房屋的面积 的数据:
的数据:
房屋面积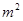 | 110 | 90 | 80 | 100 | 120 |
| 销售价格(万元) | 33 | 31 | 28 | 34 | 39 |
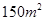 时的销售价格.
时的销售价格. ,
, 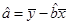 ,
,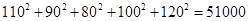 ,
,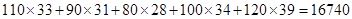 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
 | 文艺节目 | 新闻节目 | 总计 |
| 20~40岁 | 40 | 18 | 58 |
| 大于40岁 | 15 | 27 | 42 |
| 总计 | 55 | 45 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
某校为了探索一种新的教学模式,进行了一项课题实验,乙班为实验班,甲班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,成绩如下表(总分:150分):
甲班
| 成绩 | 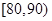 |  | 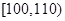 | 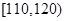 | 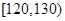 |
| 频数 | 4 | 20 | 15 | 10 | 1 |
| 成绩 | 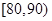 |  | 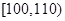 | 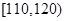 | 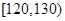 |
| 频数 | 1 | 11 | 23 | 13 | 2 |
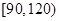 内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;
内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;| | 成绩小于100分 | 成绩不小于100分 | 合计 |
| 甲班 | 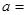 | 26 | 50 |
| 乙班 | 12 | 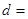 | 50 |
| 合计 | 36 | 64 | 100 |
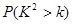 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2的列联表;
(2)判断性别与休闲方式是否有关系。
附: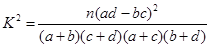 ;
;
 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com