
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为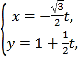 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() ,定点
,定点![]() ,点
,点![]() 是曲线
是曲线![]() 上的动点,
上的动点, ![]() 为
为![]() 的中点.
的中点.
(1)求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,若
,若![]() 的中点为
的中点为![]() ,求
,求![]() 的长.
的长.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.已知直线
轴正半轴为极轴建立极坐标系.已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过动点![]() 且平行于
且平行于![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 两点,若
两点,若![]() ,求动点
,求动点![]() 到直线
到直线![]() 的最近距离.
的最近距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程:
的参数方程: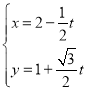 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴非负半轴为极轴(取相同单位长度)建立极坐标系,圆
轴非负半轴为极轴(取相同单位长度)建立极坐标系,圆![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(1)将直线![]() 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求圆![]() 上的点到直线
上的点到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第24届冬季奥林匹克运动会将于2022年在北京-张家口举行,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高变成如右所示的茎叶图(单位: ![]() ):若身高在
):若身高在![]() 以上(包括
以上(包括![]() )定义为“高个子”,身高在
)定义为“高个子”,身高在![]() 以下(不包括
以下(不包括![]() )定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
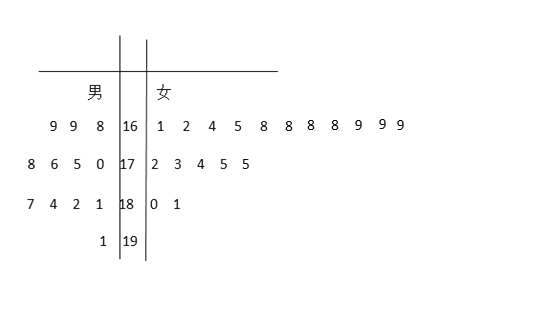
(1)如果分层抽样的方法从“高个子”和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用![]() 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,新冠病毒引发的肺炎疫情在全球肆虐,为了止损,某地一水果店老板利用抖音直播卖货,经过一段时间对一种水果的销售情况进行统计,得到![]() 天的数据如下:
天的数据如下:
销售单价 |
|
|
|
|
|
销售量 |
|
|
|
|
|
(1)建立![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)该水果店开展促销活动,当该水果销售单价为![]() 元/
元/![]() 时,其销售量达到
时,其销售量达到![]() ,若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过
,若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过![]() ,则认为所得到的回归直线方程是理想的,试问:(1)中得到的回归直线方程是否理想?
,则认为所得到的回归直线方程是理想的,试问:(1)中得到的回归直线方程是否理想?
(3)根据(1)的结果,若该水果成本是![]() 元/
元/![]() ,销售单价
,销售单价![]() 为何值时(销售单价不超过
为何值时(销售单价不超过![]() 元/
元/![]() ),该水果店利润的预计值最大?
),该水果店利润的预计值最大?
参考公式:回归直线方程![]() ,其中
,其中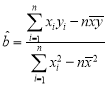 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年12月12日我国出现了新型冠状病毒所感染的肺炎,新型冠状病毒的传染性极强.下图是2020年1月26号到2月17号全国/湖北/非湖北新增新型冠状病毒感染确诊病例对比图,根据图象下列判断错误的是( )
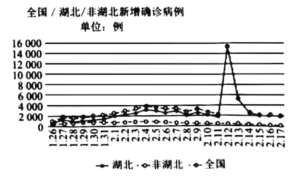
A.该时段非湖北新增感染确诊病例比湖北少
B.全国新增感染确诊病例平均数先增后减
C.2.12全国新增感染确诊病例明显增加,主要是由湖北引起的
D.2.12全国新增感染确诊病例数突然猛增,不会影响该段时期全国新增病例数的中位数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com