
 ,列表讨论得g(x)在闭区间[-3,3]上的值域为[-21,111].由f(x)在[-3,3]的值域为[-k-8,-k+120],若对于任意x1∈[-3,3],总存在x∈[-3,3]使得g(x)=f(x1)成立,知
,列表讨论得g(x)在闭区间[-3,3]上的值域为[-21,111].由f(x)在[-3,3]的值域为[-k-8,-k+120],若对于任意x1∈[-3,3],总存在x∈[-3,3]使得g(x)=f(x1)成立,知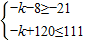 ,由此能求出k的取值范围.
,由此能求出k的取值范围. ,
,| x | -3 | (-3,-1) | -1 | (-1,- ) ) | - | (- ,3) ,3) | 3 |
| f′(x) | + | + | 0 | - | 0 | + | + |
| f(x) | ↑ | ↑ | 极大值 | ↓ | 极小值 | ↑ | ↑ |
 )=2×(-
)=2×(-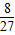 )+5×
)+5× +4×
+4×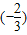 =-
=-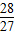 ,
,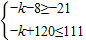 ,
,

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省上饶市上饶县中学高三(上)第一次月考数学试卷(文科)(特、零)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com