
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() :
:![]() ,直线
,直线![]() :
:![]() .
.![]() 为圆
为圆![]() 内一点,弦
内一点,弦![]() 过点
过点![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() .
.
(1)若![]() ,求
,求![]() 的面积;
的面积;
(2)判断直线![]() 与圆
与圆![]() 的位置关系,并证明.
的位置关系,并证明.
科目:高中数学 来源: 题型:
【题目】(多选题)下列说法正确的是( )
A.在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 平均减少2.3个单位
平均减少2.3个单位
B.两个具有线性相关关系的变量,当相关指数![]() 的值越接近于0,则这两个变量的相关性就越强
的值越接近于0,则这两个变量的相关性就越强
C.若两个变量的相关指数![]() ,则说明预报变量的差异有88%是由解释变量引起的
,则说明预报变量的差异有88%是由解释变量引起的
D.在回归直线方程![]() 中,相对于样本点
中,相对于样本点![]() 的残差为
的残差为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东京夏季奥运会推迟至2021年7月23日至8月8日举行,此次奥运会将设置4![]() 100米男女混泳接力赛这一新的比赛项目,比赛的规则是:每个参赛国家派出2男2女共计4名运动员参加比赛,按照仰泳
100米男女混泳接力赛这一新的比赛项目,比赛的规则是:每个参赛国家派出2男2女共计4名运动员参加比赛,按照仰泳![]() 蛙泳
蛙泳![]() 蝶泳
蝶泳![]() 自由泳的接力顺序,每种泳姿100米且由1名运动员完成,且每名运动员都要出场.若中国队确定了备战该项目的4名运动员名单,其中女运动员甲只能承担仰泳或者自由泳,男运动员乙只能承担蝶泳或者蛙泳,剩下2名运动员四种泳姿都可以承担,则中国队参赛的安排共有( )
自由泳的接力顺序,每种泳姿100米且由1名运动员完成,且每名运动员都要出场.若中国队确定了备战该项目的4名运动员名单,其中女运动员甲只能承担仰泳或者自由泳,男运动员乙只能承担蝶泳或者蛙泳,剩下2名运动员四种泳姿都可以承担,则中国队参赛的安排共有( )
A.144种B.8种C.24种D.12种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在统计学中,同比增长率一般是指和去年同期相比较的增长率,环比增长率一般是指和前一时期相比较的增长率.2020年2月29日人民网发布了我国2019年国民经济和社会发展统计公报图表,根据2019年居民消费价格月度涨跌幅度统计折线图,下列说法正确的是( )
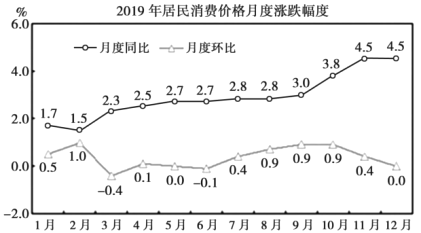
A.2019年我国居民每月消费价格与2018年同期相比有涨有跌
B.2019年我国居民每月消费价格中2月消费价格最高
C.2019年我国居民每月消费价格逐月递增
D.2019年我国居民每月消费价格3月份较2月份有所下降
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设X是有限集,t为正整数,F是包含t个子集的子集族:F=![]() .如果F中的部分子集构成的集族S满足:对S中任意两个不相等的集合A、B,
.如果F中的部分子集构成的集族S满足:对S中任意两个不相等的集合A、B,![]() 均不成立,则称S为反链.设S1为包含集合最多的反链,S2是任意反链.证明:存在S2到S1的单射f,满足
均不成立,则称S为反链.设S1为包含集合最多的反链,S2是任意反链.证明:存在S2到S1的单射f,满足![]() 或
或![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,
,![]() 为过焦点
为过焦点![]() 且垂直于
且垂直于![]() 轴的抛物线
轴的抛物线![]() 的弦,已知以
的弦,已知以![]() 为直径的圆经过点
为直径的圆经过点![]() .
.
(1)求![]() 的值及该圆的方程;
的值及该圆的方程;
(2)设![]() 为
为![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 的切线,切点为
的切线,切点为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=axlnx﹣x2﹣ax+1(a∈R)在定义域内有两个不同的极值点.
(1)求实数a的取值范围;
(2)设两个极值点分别为x1,x2,x1<x2,证明:f(x1)+f(x2)<2﹣x12+x22.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com