
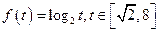 .
.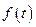 的值域G;
的值域G;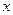 ,不等式
,不等式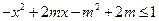 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.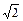 ,8]上是单调递增的,∴log2
,8]上是单调递增的,∴log2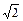 ≤log2t≤log28.
≤log2t≤log28.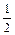 ≤f(t)≤3.∴f(t)的值域G为[
≤f(t)≤3.∴f(t)的值域G为[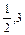 ]. -------4 分
]. -------4 分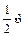 ]上恒成立
]上恒成立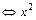 -2mx+m2-2m+1≥0在x∈[
-2mx+m2-2m+1≥0在x∈[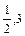 ]上恒成
]上恒成 立.-----6分
立.-----6分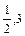 ].只需gmin(x)≥0即可.
].只需gmin(x)≥0即可.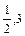 ].
]. m≤
m≤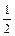 时,gmin(x)=g(
时,gmin(x)=g(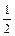 )=
)=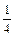 -3m+m2+1≥0.∴4m2-12m+5≥0.解得m≥
-3m+m2+1≥0.∴4m2-12m+5≥0.解得m≥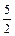 或m≤
或m≤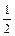
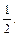
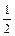 <m<3时,gmin(x)=g(m)= -2m+1≥0.解得m≤
<m<3时,gmin(x)=g(m)= -2m+1≥0.解得m≤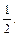 这与
这与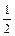 <m<3矛盾.----10
<m<3矛盾.----10  +m2-8m≥0.解得m≥4+
+m2-8m≥0.解得m≥4+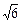 或m≤4-
或m≤4-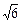 .而m≥3,
.而m≥3,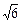 . ----12分综上,实数m的取值范围是 (-∞,
. ----12分综上,实数m的取值范围是 (-∞,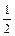 )∪[4+
)∪[4+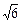 ,+∞].
,+∞].

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com