
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD= ![]() ,且点M和N分别为B1C和D1D的中点.
,且点M和N分别为B1C和D1D的中点.
(I)求证:MN∥平面ABCD;
(II)求二面角D1﹣AC﹣B1的正弦值.
【答案】证明:(1)如图,以A为原点建立空间直角坐标系,依题意A(0,0,0),B(0,1,0),C(2,0,0),D(1,﹣2,0),
A1(0,0,2),B1(0,1,2),C1(2,0,2),D1(1,﹣2,2),
又∵M,N分别为B1C和D1D的中点,∴M(1, ![]() ,1),N(1,﹣2,1).
,1),N(1,﹣2,1).
由题意得 ![]() =(0,0,1)为平面ABCD的一个法向量,
=(0,0,1)为平面ABCD的一个法向量,![]() =(0,﹣
=(0,﹣ ![]() ,0),
,0),
∵ ![]() =0,又∵直线MN平面ABCD,
=0,又∵直线MN平面ABCD,
∴MN∥平面ABCD.
(II) ![]() =(1,﹣2,2),
=(1,﹣2,2), ![]() ,设
,设 ![]() 为平面ACD1的法向量,
为平面ACD1的法向量,
则 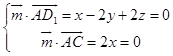 ,不妨设z=1,得
,不妨设z=1,得 ![]() =(0,1,1),
=(0,1,1),
设 ![]() 为平面ACB1的一个法向量,
为平面ACB1的一个法向量, ![]() =(0,1,2),
=(0,1,2),
则 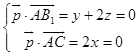 ,不妨设z=1,得
,不妨设z=1,得 ![]() =(0,﹣2,1),
=(0,﹣2,1),
∴cos< ![]() >=
>= ![]() =﹣
=﹣ ![]() ,于是sin<
,于是sin< ![]() >=
>= 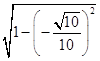 =
= ![]() ,
,
∴二面角D1﹣AC﹣B1的正弦值为 ![]() .
.
【解析】(Ⅰ)以A为原点建立空间直角坐标系,利用向量法能证明MN∥平面ABCD.(Ⅱ)求出两个平面的法向量,可计算两个平面所成二面角的余弦值的大小,再求正弦值即可.
【考点精析】认真审题,首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行).


科目:高中数学 来源: 题型:
【题目】已知公差不为0的等差数列{an}中,a1=2,且a2+1,a4+1,a8+1成等比数列.
(1)求数列{an}通项公式;
(2)设数列{bn}满足bn= ![]() ,求适合方程b1b2+b2b3+…+bnbn+1=
,求适合方程b1b2+b2b3+…+bnbn+1= ![]() 的正整数n的值.
的正整数n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于不等式![]() ,则对区间
,则对区间![]() 上的任意x都成立的实数t的取值范围是_______.
上的任意x都成立的实数t的取值范围是_______.
【答案】![]()
【解析】
根据二次函数的单调性求出x2﹣3x+2在区间[0,2]上的最小值和最大值,把问题转化关于t的不等式组 得答案.
得答案.
∵x2﹣3x+2=![]() ,
,
∴当x∈[0,2]时,![]() ,(x2﹣3x+2)max=2.
,(x2﹣3x+2)max=2.
∴ .
.
∴对于不等式![]() (2t﹣t2)≤x2﹣3x+2≤3﹣t2,对区间[0,2]上任意x都成立的实数t的取值范围是[﹣1,1﹣
(2t﹣t2)≤x2﹣3x+2≤3﹣t2,对区间[0,2]上任意x都成立的实数t的取值范围是[﹣1,1﹣![]() ].
].
故答案为:[﹣1,1﹣![]() ].
].
【点睛】
本题考查函数恒成立问题,考查了不等式的解法,体现了数学转化思想方法,是基础题.二次不等式分含参二次不等式和不含参二次不等式;对于含参的二次不等式问题,先判断二次项系数是否含参,接着讨论参数等于0,不等于0,再看式子能否因式分解,若能够因式分解则进行分解,再比较两根大小,结合图像得到不等式的解集.
【题型】填空题
【结束】
16
【题目】等差数列{an}的公差d≠0满足![]() 成等比数列,若
成等比数列,若![]() =1,Sn是{
=1,Sn是{![]() }的前n项和,则
}的前n项和,则![]() 的最小值为________.
的最小值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是公比为正数的等比数列,
是公比为正数的等比数列,![]() ,
,![]()
(1)求![]() 的通项公式;
的通项公式;
(2)设![]() 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列![]() 的前
的前![]() 项和
项和![]()
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)![]() 根据等比数列的通项公式得到:
根据等比数列的通项公式得到:![]() ,解得二次方程可得到
,解得二次方程可得到![]() 或
或![]() (舍去),进而得到数列的通项;(2)已知数列的类型是等差数列与等比数列求和的问题,根据等差等比数列求和公式得到结果即可.
(舍去),进而得到数列的通项;(2)已知数列的类型是等差数列与等比数列求和的问题,根据等差等比数列求和公式得到结果即可.
解:(1)设![]() 为等比数列
为等比数列![]() 的公比,则由
的公比,则由![]() ,
,![]() 得:
得:![]()
即![]() ,解得:
,解得:![]() 或
或![]() (舍去)
(舍去)
所以![]() 的通项公式为
的通项公式为![]()
(2) 由 等 差 数 列 的 通 项 公 式 得 到:![]()
由 等 差 数 列求 和 公 式 和 等 比 数 列 前 n 项 和 公 式 得 到
![]()
【点睛】
这个题目考查的是数列通项公式的求法及数列求和的常用方法;数列通项的求法中有常见的已知![]() 和
和![]() 的关系,求
的关系,求![]() 表达式,一般是写出
表达式,一般是写出![]() 做差得通项,但是这种方法需要检验n=1时通项公式是否适用;数列求和常用法有:错位相减,裂项求和,分组求和等。
做差得通项,但是这种方法需要检验n=1时通项公式是否适用;数列求和常用法有:错位相减,裂项求和,分组求和等。
【题型】解答题
【结束】
18
【题目】设a≠b,解关于x的不等式a2x+b2(1-x)≥[ax+b(1-x)]2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线C1的参数方程为![]() (θ为参数),将曲线C1上所有点的横坐标伸长为原来的2倍,纵坐标伸长为原来的
(θ为参数),将曲线C1上所有点的横坐标伸长为原来的2倍,纵坐标伸长为原来的![]() 倍,得到曲线C2.以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(cosθ-2sinθ)=6.
倍,得到曲线C2.以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(cosθ-2sinθ)=6.
(1)求曲线C2和直线l的普通方程.
(2)P为曲线C2上任意一点,求点P到直线l的距离的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1至9这9个自然数中任取两个:
![]() 恰有一个偶数和恰有一个奇数;
恰有一个偶数和恰有一个奇数;![]() 至少有一个是奇数和两个数都是奇数;
至少有一个是奇数和两个数都是奇数;
![]() 至多有一个奇数和两个数都是奇数;
至多有一个奇数和两个数都是奇数;![]() 至少有一个奇数和至少有一个偶数.
至少有一个奇数和至少有一个偶数.
在上述事件中,是对立事件的是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中装有![]() 个红球
个红球![]() 且
且![]() 和
和![]() 个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
(1)用![]() 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率![]() ;
;
(2)若![]() ,设三次摸奖(每次摸奖后球放回)恰好有
,设三次摸奖(每次摸奖后球放回)恰好有![]() 次中奖,求
次中奖,求![]() 的数学期望
的数学期望![]() ;
;
(3)设三次摸奖(每次摸奖后球放回)恰好有一次中奖的概率![]() ,当
,当![]() 取何值时,
取何值时, ![]() 最大?
最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com