
【题目】已知函数f(x)= ![]() x2﹣ax﹣1,x∈[﹣5,5]
x2﹣ax﹣1,x∈[﹣5,5]
(1)当a=2,求函数f(x)的最大值和最小值;
(2)若函数f(x)在定义域内是单调函数,求a的取值范围.
【答案】
(1)解:当a=2时,函数f(x)= ![]() x2﹣2x﹣1的图象是开口朝上,且以直线x=2为对称轴的抛物线,
x2﹣2x﹣1的图象是开口朝上,且以直线x=2为对称轴的抛物线,
由x∈[﹣5,5]得:
当x=﹣5时,函数取最大值 ![]() ,
,
当x=2时,函数取最小值﹣3
(2)解:函数f(x)= ![]() x2﹣ax﹣1的图象是开口朝上,且以直线x=a为对称轴的抛物线,
x2﹣ax﹣1的图象是开口朝上,且以直线x=a为对称轴的抛物线,
若函数f(x)在定义域内是单调函数,
则a≤﹣5,或a≥5
【解析】(1)当a=2时,函数f(x)= ![]() x2﹣2x﹣1的图象是开口朝上,且以直线x=2为对称轴的抛物线,由x∈[﹣5,5]可得函数的最值;(2)函数f(x)在定义域内是单调函数,则a≤﹣5,或a≥5.
x2﹣2x﹣1的图象是开口朝上,且以直线x=2为对称轴的抛物线,由x∈[﹣5,5]可得函数的最值;(2)函数f(x)在定义域内是单调函数,则a≤﹣5,或a≥5.
【考点精析】本题主要考查了函数单调性的判断方法和函数的最值及其几何意义的相关知识点,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A、B、C所对的边分别为a,b,c且a=5,sinA= ![]() .
.
(I)若S△ABC= ![]() ,求周长l的最小值;
,求周长l的最小值;
(Ⅱ)若cosB= ![]() ,求边c的值.
,求边c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (a>0).
(a>0).
(1)证明:当x>0时,f(x)在 ![]() 上是减函数
上是减函数 ![]() ,在上是增函数,并写出当x<0时f(x)的单调区间;
,在上是增函数,并写出当x<0时f(x)的单调区间;
(2)已知函数 ![]() ,函数g(x)=﹣x﹣2b,若对任意x1∈[1,3],总存在x2∈[1,3],使得g(x2)=h(x1)成立,求实数b的取值范围.
,函数g(x)=﹣x﹣2b,若对任意x1∈[1,3],总存在x2∈[1,3],使得g(x2)=h(x1)成立,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 已知2Sn=3n+3.
(Ⅰ)求{an}的通项公式;
(Ⅱ)若数列{bn},满足anbn=log3an , 求{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)是定义在D上的函数,若存在区间[m,n]D,使函数f(x)在[m,n]上的值域恰为[km,kn],则称函数f(x) 是k型函数.给出下列说法:
①f(x)=3﹣ ![]() 不可能是k型函数;
不可能是k型函数;
②若函数y=﹣ ![]() x2+x是3型函数,则m=﹣4,n=0;
x2+x是3型函数,则m=﹣4,n=0;
③设函数f(x)=x3+2x2+x(x≤0)是k型函数,则k的最小值为 ![]() ;
;
④若函数y= ![]() (a≠0)是1型函数,则n﹣m的最大值为
(a≠0)是1型函数,则n﹣m的最大值为 ![]() .
.
下列选项正确的是( )
A.①③
B.②③
C.②④
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
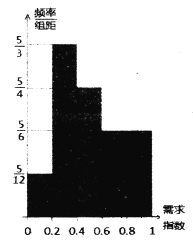
【题目】某公司每个工作日由位于市区的总公司向位于郊区的分公司开一个来回的班车(每年按200个工作日计算),现有两种使用班车的方案,方案一是购买一辆大巴,需花费90万元,报废期为10年,车辆平均每年的各种费用合计5万元,司机年工资6万元,司机每天请假的概率为0.1(每年请假时间不超过15天不扣工资,超过15天每天100元),若司机请假则需从公交公司雇佣司机,每天支付300元工资.方案二是租用公交公司的车辆(含司机),根据调研每年12个月的车辆需求指数如直方图所示,其中当某月车辆需求指数在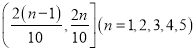 时,月租金为
时,月租金为![]() 万元.
万元.
(1)若购买大巴,设司机每年请假天数为![]() ,求公司因司机请假而增加的花费
,求公司因司机请假而增加的花费![]() (元)及使用班车年平均花费
(元)及使用班车年平均花费![]() (万元)的数学期望
(万元)的数学期望![]() .
.
(2)试用调研数据,给出公司使用班车的建议,使得年平均花费最少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com