
【题目】在正方体ABCD-A1B1C1D1中,M、N分别是AB、BC的中点.

(1)求证:MN∥平面A1B1C1D1
(2)求证:平面B1MN⊥平面BB1D1D.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知直线![]() :
:![]() ,点
,点![]() .
.
(1)求点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 的坐标;
的坐标;
(2)直线![]() 关于点
关于点![]() 对称的直线
对称的直线![]() 的方程;
的方程;
(3)以![]() 为圆心,3为半径长作圆,直线
为圆心,3为半径长作圆,直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
(1)请在图中画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测记忆力为9的同学的判断力.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,且
为参数,且![]() ),以
),以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线 ![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若曲线![]() 与
与![]() 只有一个公共点,求
只有一个公共点,求![]() 的值;
的值;
(2)![]() ,
, ![]() 为曲线
为曲线![]() 上的两点,且
上的两点,且![]() ,求△
,求△![]() 的面积最大值.
的面积最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年1月1日,我国实行全面二孩政策,同时也对妇幼保健工作提出了更高的要求.某城市实行网格化管理,该市妇联在网格1与网格2两个区域内随机抽取12个刚满8个月的婴儿的体重信息,体重分布数据的茎叶图如图所示(单位:斤,2斤![]() 1千克),体重不超过
1千克),体重不超过![]() 千克的为合格.
千克的为合格.

(1)从网格1与网格2分别随机抽取2个婴儿,求网格1至少有一个婴儿体重合格且网格2至少有一个婴儿体重合格的概率;
(2)妇联从网格1内8个婴儿中随机抽取4个进行抽检,若至少2个婴儿合格,则抽检通过,若至少3个合格,则抽检为良好,求网格1在抽检通过的条件下,获得抽检为良好的概率;
(3)若从网格1与网格2内12个婴儿中随机抽取2个,用![]() 表示网格2内婴儿的个数,求
表示网格2内婴儿的个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
(Ⅰ)根据以上资料完成下面的2×2列联表,若据此数据算得![]() ,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?
,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?

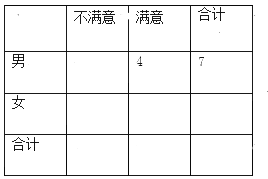
附:

(Ⅱ) 估计用户对该公司的产品“满意”的概率;
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形(记为Q).
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P是直线x=﹣4与x轴的交点,过点P的直线l与椭圆C相交于M,N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线l斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛掷一个质地均匀的骰子的试验,事件A表示“小于5的偶数点出现”,事件B表示“不小于5的点数出现”,则一次试验中,事件A或事件B至少有一个发生的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市为调查会员某年度上半年的消费情况制作了有奖调查问卷发放给所有会员,并从参与调查的会员中随机抽取![]() 名了解情况并给予物质奖励.调查发现抽取的
名了解情况并给予物质奖励.调查发现抽取的![]() 名会员消费金额(单位:万元)都在区间
名会员消费金额(单位:万元)都在区间![]() 内,调查结果按消费金额分成
内,调查结果按消费金额分成![]() 组,制作成如下的频率分布直方图.
组,制作成如下的频率分布直方图.
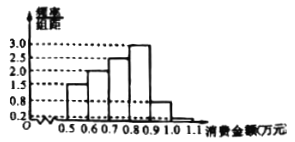
(1)求该![]() 名会员上半年消费金额的平均值与中位数;(以各区间的中点值代表该区间的均值)
名会员上半年消费金额的平均值与中位数;(以各区间的中点值代表该区间的均值)
(2)现采用分层抽样的方式从前![]() 组中选取
组中选取![]() 人进行消费爱好调查,然后再从前
人进行消费爱好调查,然后再从前![]() 组选取的人中随机选
组选取的人中随机选![]() 人,求这
人,求这![]() 人都来自第
人都来自第![]() 组的概率.
组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com