
分析 由题意可得$\overrightarrow{PB}•\overrightarrow{PD}$=($\overrightarrow{PA}$+$\overrightarrow{AB}$)•($\overrightarrow{PA}$+$\overrightarrow{AD}$),再利用两个向量的数量积的定义,余弦定理求得它的值.
解答 解:由题意可得$\overrightarrow{PB}•\overrightarrow{PD}$=($\overrightarrow{PA}$+$\overrightarrow{AB}$)•($\overrightarrow{PA}$+$\overrightarrow{AD}$)=${\overrightarrow{PA}}^{2}$+$\overrightarrow{PA}$•$\overrightarrow{AD}$+$\overrightarrow{AB}•\overrightarrow{PA}$+$\overrightarrow{AB}•\overrightarrow{AD}$
=9+$\overrightarrow{PA}$•($\overrightarrow{AD}$+$\overrightarrow{AB}$)+0=9+$\overrightarrow{PA}•\overrightarrow{AC}$=9+3•6•cos(π-∠PAC)=9-18•$\frac{{PA}^{2}{+AC}^{2}{-PC}^{2}}{2•PA•AC}$
=9-18•$\frac{9+36-16}{2•3•6}$=-$\frac{11}{2}$,
故答案为:$-\frac{11}{2}$.
点评 本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义、余弦定理,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (9,49) | B. | (13,49) | C. | (9,25) | D. | (3,7) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
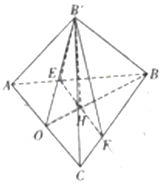 如图,等腰△ABC中,AB=BC=5,AC=6,点E,F分别在AB,BC上,AE=CF=$\frac{5}{4}$,O为AC边上的中点,EF交BO于点H,将△BEF沿EF折到△B′EF的位置,OB′=$\sqrt{10}$.
如图,等腰△ABC中,AB=BC=5,AC=6,点E,F分别在AB,BC上,AE=CF=$\frac{5}{4}$,O为AC边上的中点,EF交BO于点H,将△BEF沿EF折到△B′EF的位置,OB′=$\sqrt{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相交过圆心 | B. | 相交 | C. | 相切 | D. | 相离 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com