
【题目】长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点. 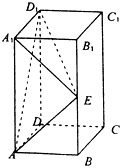
(1)求证:直线AE⊥平面A1D1E;
(2)求二面角E﹣AD1﹣A1的平面角的余弦值.
【答案】
(1)证明:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
A(1,0,0),E(1,1,1),A1(1,0,2),D1(0,0,2),
![]() =(0,1,1),
=(0,1,1), ![]() =(0,1,﹣1),
=(0,1,﹣1), ![]() =(﹣1,0,0),
=(﹣1,0,0),
![]() =0,
=0, ![]() =0,
=0,
∵AE⊥A1E,AE⊥A1D1,
∵A1E∩A1D1=A1,∴直线AE⊥平面A1D1E.
(2)解: ![]() =(0,1,1),
=(0,1,1), ![]() =(﹣1,0,2),
=(﹣1,0,2),
设平面AED1的法向量 ![]() =(x,y,z),
=(x,y,z),
则 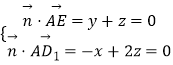 ,取x=2,得
,取x=2,得 ![]() =(2,﹣1,1),
=(2,﹣1,1),
又平面A1D1A的法向量 ![]() =(0,1,0),
=(0,1,0),
设二面角E﹣AD1﹣A1的平面角的平面角为θ,
则cosθ= ![]() =
= ![]() =
= ![]() .
.
∴二面角E﹣AD1﹣A1的平面角的余弦值为 ![]() .
.
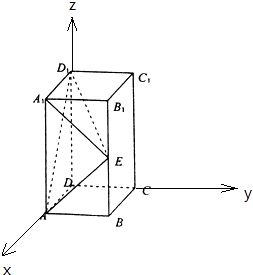
【解析】(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能证明直线AE⊥平面A1D1E.(2)求出平面AED1的法向量和平面A1D1A的法向量,利用向量法能求出二面角E﹣AD1﹣A1的平面角的余弦值.
【考点精析】本题主要考查了直线与平面垂直的判定的相关知识点,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,AA1=12,
点D是AB的中点.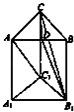
(1)求证:AC⊥B1C
(2)求证:AC1∥平面CDB1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头,它们在一昼夜内任何时刻到达是等可能的.
(1)已知甲船上有男女乘客各3名,现从中任选3人出来做某件事情,求所选出的人中恰有一位女乘客的概率;
(2)如果甲船的停泊时间为4小时,乙船的停泊时间为2小时,求它们中的任何一条船不需要等待码头空出的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
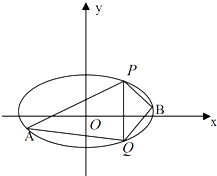
【题目】已知椭圆C的中心在原点,焦点在x轴上,离心率等于 ![]() ,它的一个短轴端点是(0,2
,它的一个短轴端点是(0,2 ![]() ).
). 
(1)求椭圆C的方程;
(2)P(2,3)、Q(2,﹣3)是椭圆上两点,A、B是椭圆位于直线PQ两侧的两动点,
①若直线AB的斜率为 ![]() ,求四边形APBQ面积的最大值;
,求四边形APBQ面积的最大值;
②当A、B运动时,满足∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(﹣∞,+∞)上的奇函数,当x>0时,f(x)=4x﹣x2 , 若函数f(x)在区间[t,4]上的值域为[﹣4,4],则实数t的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆的中心在原点O,短轴长为 ![]() ,左焦点为F(﹣c,0)(c>0),直线
,左焦点为F(﹣c,0)(c>0),直线 ![]() 与x轴交于点A,且
与x轴交于点A,且 ![]() ,过点A的直线与椭圆相交于P,Q两点.
,过点A的直线与椭圆相交于P,Q两点. 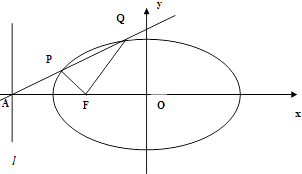
(1)求椭圆的方程.
(2)若 ![]() ,求直线PQ的方程.
,求直线PQ的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+)( ![]() )的部分图象如图所示.
)的部分图象如图所示. 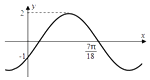
(1)求函数f(x)的解析式.
(2)函数y=f(x)的图象可以由y=sinx的图象变换后得到,请写出一种变换过程的步骤(注明每个步骤后得到新的函数解析式).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com