第一行是等差数列0,1,2,3,…,2008,将其相邻两项的和依次写下作为第二行,第二行相邻两项的和依次写下作为第三行,依此类推,共写出2008行.
0,1,2,3,…,2005,2006,2007,2008
1,3,5,…,4011,4013,4015
4,8,…,8024,8028
…
(1)由等差数列性质知,以上数表的每一行都是等差数列.记各行的公差组成数列{di}(i=1,2,3…,2008).求通项公式di;
(2)各行的第一个数组成数列{bi}(1,2,3,…,2008),求数列{bi}所有各项的和.
【答案】
分析:(1)记a
i•j表示第i行第j列的项,求出 d
i+1=2d
i,可得{d
i}是等比数列,d
i=d
1•2
i-1=2
i-1.
(2)化简b
i+1=a
i1+a
i2=2b
i+2
i-1,可得
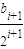
=

+

,得数列{

}是等差数列,b
i=

(i-1)2
i=(i-1)2
i-2,数列{b
i}所有各项的和S=0+1+2×2+3×2
2+…+2007×2
2006,用错位相减法,得到S的值.
解答:解. (1)记a
i•j表示第i行第j列的项,
∵d
i+1=a
(i+1)•(k+1)-a
(i+1)•k =a
i•(k+1)+a
i•(k+2)-a
i•k-a
i•(k+1)=a
i•(k+2)-a
i•k=2d
i,
∴

=2,则{d
i}是等比数列,d
i=d
1•2
i-1=2
i-1.
(2)b
i+1=a
i1+a
i2=a
i1+a
i1+d
i=2a
i1+2
i-1=2b
i+2
i-1,∴

=
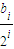
+

.
∴数列{

}是等差数列,

=

(i-1),所以 b
i=

(i-1)2
i=(i-1)2
i-2,
设数列{b
i}所有各项的和S,则 S=0+1+2×2+3×2
2+…+2007×2
2006 ①,
∴2 S=0+1×2+2×2
2+3×2
3+…+2007×2
2007 ②,
用①-②可得-S=-1003×2
2008-1.
从而得到S=1003×2
2008 +1.
点评:本题是中档题,考查数列的有关知识,证明数列是等差数列,数列的递推关系式的应用,数列与函数的综合应用,
考查计算能力,属于中档题.

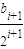 =
= +
+ ,得数列{
,得数列{ }是等差数列,bi=
}是等差数列,bi= (i-1)2i=(i-1)2i-2,数列{bi}所有各项的和S=0+1+2×2+3×22+…+2007×22006,用错位相减法,得到S的值.
(i-1)2i=(i-1)2i-2,数列{bi}所有各项的和S=0+1+2×2+3×22+…+2007×22006,用错位相减法,得到S的值. =2,则{di}是等比数列,di=d1•2i-1=2i-1.
=2,则{di}是等比数列,di=d1•2i-1=2i-1. =
=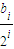 +
+ .
. }是等差数列,
}是等差数列, =
= (i-1),所以 bi=
(i-1),所以 bi= (i-1)2i=(i-1)2i-2,
(i-1)2i=(i-1)2i-2,


