(Ⅰ)解:将x=3代入直线方程得
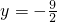
,
∵点(3,f(3))在函数f(x)=ax
3+bx
2的图象上,∴
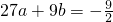
①
由f'(x)=3ax
2+2bx,f'(3)=-6,∴27a+6b=-6②
联立①②,解得
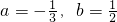
.
∴
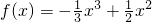
;
(Ⅱ)解:由f'(x)=-x
2+x,∴对任意的x∈[0,+∞),f'(x)≤kln(x+1)恒成立,
即-x
2+x≤kln(x+1)在x∈[0,+∞)上恒成立;
也就是x
2-x+kln(x+1)≥0在x∈[0,+∞)恒成立;
设g(x)=x
2-x+kln(x+1),g(0)=0,
∴只需对于任意的x∈[0,+∞)有g(x)≥g(0)即可.
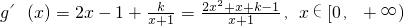
设h(x)=2x
2+x+k-1,
(1)当△=1-8(k-1)≤0,即
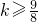
时,h(x)≥0,∴g'(x)≥0,∴g(x)在[0,+∞)单调递增,
∴g(x)≥g(0)
(2)当△=1-8(k-1)>0,即
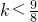
时,设
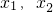
是方程2x
2+x+k-1=0的两根且x
1<x
2由
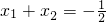
,可知x
1<-

,
要使对任意x∈[0,+∞)有g(x)≥g(0),只需
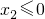
,
即k-1≥0,∴k≥1,∴
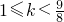
综上分析,实数k的最小值为1.
(Ⅲ)证明:因为当k=1时,有f'(x)≤kln(x+1)恒成立,即-x
2+x≤ln(x+1),也就是x≤x
2+ln(x+1)在x∈[0,+∞)恒成立;
令
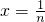
,得
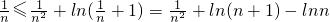
.
∴
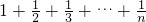
≤
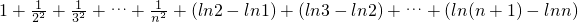
=
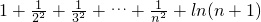
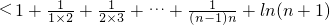
=
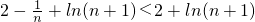
.
∴原不等式得证.
分析:(Ⅰ)由点(3,f(3))在切线上,可求点的纵坐标,又在曲线上,把求得的点的坐标代入曲线方程可得一个关于a,b的方程,再根据函数在点(3,f(3))处的切线的斜率列关于a,b的第二个方程,联立后即可求得a,b的值,则函数解析式可求;
(Ⅱ)求出函数的导函数后代入f′(x)≤kln(x+1),把对任意的x∈[0,+∞),f′(x)≤kln(x+1)恒成立转化为x
2-x+klnx≥0在x∈[0,+∞)恒成立,引入辅助函数g(x)=x
2-x+kln(x+1),而g(0)=0,则问题转化为函数g(x)=x
2-x+kln(x+1)在[0,+∞)上为增函数,求k的值.把函数g(x)求导后,通过满足导函数在[0,+∞)上恒大于等于0可求实数k的取值范围.
(Ⅲ)当k=1时,(Ⅱ)中的结论变为-x
2+x≤ln(x+1),也就是x≤x
2+ln(x+1)在x∈[0,+∞)恒成立,取
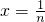
后利用对数式的性质展开,作和后先放缩再裂项,整理即可得到结论.
点评:本题考查了利用导数研究函数的切线方程问题,在曲线上某点处的切线的斜率就是该点的导数值,考查了导数在最大值和最小值中的应用,体现了数学转化思想和分类讨论的数学思想.特别是(Ⅲ)的证明,用到了放缩法和裂项相消,此题属难度较大的题目.

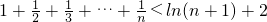 (n∈N*).
(n∈N*).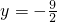 ,
,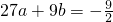 ①
①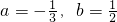 .
.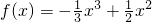 ;
;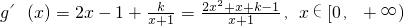
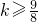 时,h(x)≥0,∴g'(x)≥0,∴g(x)在[0,+∞)单调递增,
时,h(x)≥0,∴g'(x)≥0,∴g(x)在[0,+∞)单调递增,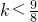 时,设
时,设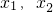 是方程2x2+x+k-1=0的两根且x1<x2
是方程2x2+x+k-1=0的两根且x1<x2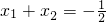 ,可知x1<-
,可知x1<- ,
,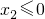 ,
,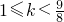
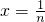 ,得
,得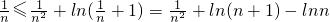 .
.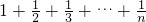 ≤
≤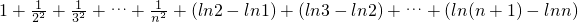
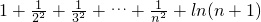
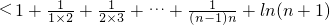
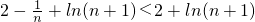 .
.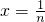 后利用对数式的性质展开,作和后先放缩再裂项,整理即可得到结论.
后利用对数式的性质展开,作和后先放缩再裂项,整理即可得到结论.
