
【题目】命题p: ![]() =1表示双曲线方程,命题q:函数f(m)=
=1表示双曲线方程,命题q:函数f(m)= ![]() 有意义.若p∨q为真,p∧q为假,求实数m的取值范围.
有意义.若p∨q为真,p∧q为假,求实数m的取值范围.
【答案】解:命题p为真,则(m+4)(m﹣2)<0,∴﹣4<m<2…(3分) 命题q为真,则m<﹣2…(6分)
∵p∨q为真,p∧q为假,则p,q一真一假
∴ ![]() 或
或  ,
,
∴所求m的取值范围为m≤﹣4或﹣2≤m<2
【解析】求出两个命题为真命题时,m的范围,然后通过p∨q为真,p∧q为假,求解即可.
【考点精析】根据题目的已知条件,利用复合命题的真假和命题的真假判断与应用的相关知识可以得到问题的答案,需要掌握“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真;两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 上一点,
上一点, ![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
, ![]() 到
到![]() 的准线的距离为
的准线的距离为![]() ,且
,且![]() 的最小值为
的最小值为![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)直线![]() 交
交![]() 于点
于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,线段
,线段![]() 的中点分别为
的中点分别为![]() ,若
,若![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求证:直线
,求证:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1927年德国汉堡大学的学生考拉兹提出一个猜想:对于每一个正整数,如果它是奇数,对它乘3再加1,如果它是偶数,对它除以2,这样循环,最终结果都能得到1.该猜想看上去很简单,但有的数学家认为“该猜想任何程度的解决都是现代数学的一大进步,将开辟全新的领域至于如此简单明了的一个命题为什么能够开辟一个全新的领域,这大概与它其中蕴含的奇偶归一思想有关.如图是根据考拉兹猜想设计的一个程序框图,则①处应填写的条件及输出的结果![]() 分别为
分别为
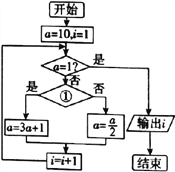
A. ![]() 是偶数?;6 B.
是偶数?;6 B. ![]() 是偶数?;8
是偶数?;8
C. ![]() 是奇数?;5 D.
是奇数?;5 D. ![]() 是奇数?;7
是奇数?;7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中, ![]() 为正三角形,平面
为正三角形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积;
的体积;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请确定点
?若存在,请确定点![]() 的位置并证明;若不存在,说明理由.
的位置并证明;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 等比数列{bn}的各项均为正数,满足:a1=b1=1,a5=b3 , 且S3=9.
(1)求数列{an}和{bn}的通项公式;
(2)求 ![]() +
+ ![]() +…+
+…+ ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设平面直角坐标系xOy中,曲线G:y= ![]() +
+ ![]() x﹣a2(x∈R),a为常数.
x﹣a2(x∈R),a为常数.
(1)若a≠0,曲线G的图象与两坐标轴有三个交点,求经过这三个交点的圆C的一般方程;
(2)在(1)的条件下,求圆心C所在曲线的轨迹方程;
(3)若a=0,已知点M(0,3),在y轴上存在定点N(异于点M)满足:对于圆C上任一点P,都有 ![]() 为一常数,试求所有满足条件的点N的坐标及该常数.
为一常数,试求所有满足条件的点N的坐标及该常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() =(2sinx,cosx+sinx),
=(2sinx,cosx+sinx), ![]() =(cosx,cosx﹣sinx),f(x)=
=(cosx,cosx﹣sinx),f(x)= ![]()
![]() .
.
(1)求函数f(x)的单调区间;
(2)若关于x的方程f(x)﹣m=0(m∈R)在区间(0, ![]() )内有两个不相等的实数根x1 , x2 , 记t=mcos(x1+x2),求实数t的取值范围.
)内有两个不相等的实数根x1 , x2 , 记t=mcos(x1+x2),求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com