
【题目】如图,在四棱锥S﹣ABCD中,AB⊥AD,AB∥CD,CD=3AB,平面SAD⊥平面ABCD,M是线段AD上一点,AM=AB,DM=DC,SM⊥AD. (Ⅰ)证明:BM⊥平面SMC;
(Ⅱ)若SB与平面ABCD所成角为 ![]() ,N为棱SC上的动点,当二面角S﹣BM﹣N为
,N为棱SC上的动点,当二面角S﹣BM﹣N为 ![]() 时,求
时,求 ![]() 的值.
的值.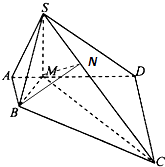
【答案】解:(Ⅰ)证明:∵平面SAD⊥平面ABCD,SM⊥AD ∴SM⊥平面ABCD,又BM平面ABCD
∴SM⊥BM
又AM=AB,DM=DC
∴∠BMA=∠DMC= ![]() ,
,
∴∠BMC= ![]() ,即CM⊥BM,
,即CM⊥BM,
又SM平面SMC,MC平面SMC,SM∩MC=M,
∴BM⊥平面SMC.
(Ⅱ)∵SM⊥平面ABCD,∴∠SBM为SB与平面ABCD所成的角,
∴∠SBM= ![]() .∴SM=BM.
.∴SM=BM.
由(1)得BM⊥平面SMC,∵MN平面SMC,
∴BM⊥MN,又BM⊥SM,
∴∠SMN为二面角S﹣BM﹣N的平面角.即∠SMN= ![]() .
.
设AB=1,则SM=BM= ![]() ,DM=DC=3,∴MC=3
,DM=DC=3,∴MC=3 ![]() .
.
∴SC= ![]() =2
=2 ![]() .sin∠MSN=
.sin∠MSN= ![]() .cos∠MSN=
.cos∠MSN= ![]() .
.
∴sin∠SNM=sin(∠MSN+∠SMN)= ![]() =
= ![]() .
.
在△SMN中,由正弦定理得 ![]() =
= ![]() ,
,
∴SN= ![]() =
= ![]() .
.
∴ ![]() ,∴
,∴ ![]() .
.
【解析】(I)利用平面几何知识证明BM⊥MC,结合SM⊥平面ABCD可得SM⊥BM,于是BM⊥平面SMC;(II)设AB=1,利用∠SBM= ![]() ,∠SMN=
,∠SMN= ![]() 可求出SM,SC,在△SMN中使用正弦定理求出SN,即可得出
可求出SM,SC,在△SMN中使用正弦定理求出SN,即可得出 ![]() 的值.
的值.
【考点精析】掌握直线与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


科目:高中数学 来源: 题型:
【题目】某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:
近视度数 | 0﹣100 | 100﹣200 | 200﹣300 | 300﹣400 | 400以上 |
学生频数 | 30 | 40 | 20 | 10 | 0 |
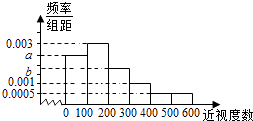
将近视程度由低到高分为4个等级:当近视度数在0﹣100时,称为不近视,记作0;当近视度数在100﹣200时,称为轻度近视,记作1;当近视度数在200﹣400时,称为中度近视,记作2;当近视度数在400以上时,称为高度近视,记作3.
(1)从该校任选1名高二学生,估计该生近视程度未达到中度及以上的概率;
(2)设a=0.0024,从该校任选1名高三学生,估计该生近视程度达到中度或中度以上的概率;
(3)把频率近似地看成概率,用随机变量X,Y分别表示高二、高三年级学生的近视程度,若EX=EY,求b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额资料如表:
商店名称 | A | B | C | D | E |
销售额x/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额y/百万元 | 2 | 3 | 3 | 4 | 5 |
(1)画出销售额和利润额的散点图;
(2)若销售额和利润额具有相关关系,用最小二乘法计算利润额y对销售额x的回归直线方程;
(3)据(2)的结果估计当销售额为1亿元时的利润额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为选拔参加“央视猜灯谜大赛”的队员,在校内组织猜灯谜竞赛.规定:第一阶段知识测试成绩不小于![]() 分的学生进入第二阶段比赛.现有
分的学生进入第二阶段比赛.现有![]() 名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
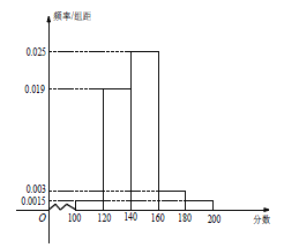
(1)估算这![]() 名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
(2)将进入第二阶段的学生分成若干队进行比赛.现甲、乙两队在比赛中均已获得![]() 分,进入最后强答阶段.抢答规则:抢到的队每次需猜
分,进入最后强答阶段.抢答规则:抢到的队每次需猜![]() 条谜语,猜对
条谜语,猜对![]() 条得
条得![]() 分,猜错
分,猜错![]() 条扣
条扣![]() 分.根据经验,甲队猜对每条谜语的概率均为
分.根据经验,甲队猜对每条谜语的概率均为![]() ,乙队猜对每条谜语的概率均为
,乙队猜对每条谜语的概率均为![]() ,猜对第
,猜对第![]() 条的概率均为
条的概率均为![]() .若这两条抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
.若这两条抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2﹣ax,g(x)=lnx,h(x)=f(x)+g(x)
(1)若f(x)≥g(x)对于公共定义域内的任意x恒成立,求实数a的取值范围;
(2)设h(x)有两个极值点x1 , x2 , 且x1∈(0, ![]() ),若h(x1)﹣h(x2)>m恒成立,求实数m的最大值.
),若h(x1)﹣h(x2)>m恒成立,求实数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体EF﹣ABCD中,CDEF为边长为2的正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,AD=2,AB=4,∠ADF=90°.

(Ⅰ)求证:AC⊥FB
(Ⅱ)求二面角E﹣FB﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对二次函数f(x)=ax2+bx+c(a为非零整数),四位同学分别给出下列结论,其中有且只有一个结论是错误的,则错误的结论是( )
A.﹣1是f(x)的零点
B.1是f(x)的极值点
C.3是f(x)的极值
D.点(2,8)在曲线y=f(x)上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{bn}满足bn=3bn﹣1+2(n≥2),b1=1.数列{an}的前n项和为Sn , 满足Sn=4an+2
(1)求证:{bn+1}是等比数列并求出数列{bn}的通项公式;
(2)求数列{an}的通项公式和前n项和公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com