【题目】如图，F1、F2是双曲线 
=1（a＞0）的左、右焦点，过F1的直线l与双曲线交于点A、B，若△ABF2为等边三角形，则△BF1F2的面积为（ ） 
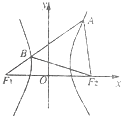
A.8
B.8 
C.8 
D.16
【答案】C
【解析】解：根据双曲线的定义，可得|BF1|﹣|BF2|=2a， ∵△ABF2是等边三角形，即|BF2|=|AB|
∴|BF1|﹣|BF2|=2a，即|BF1|﹣|AB|=|AF1|=2a
又∵|AF2|﹣|AF1|=2a，
∴|AF2|=|AF1|+2a=4a，
∵△AF1F2中，|AF1|=2a，|AF2|=4a，∠F1AF2=120°
∴|F1F2|2=|AF1|2+|AF2|2﹣2|AF1||AF2|cos120°
即4c2=4a2+16a2﹣2×2a×4a×（﹣ 
）=28a2 ， 解之得c= 
a，
∴a2+24=7a2 ， ∴a=2，
∴△BF1F2的面积为 
﹣ 
= 
﹣ 
=8 
．
故选：C．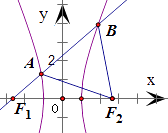
科目：高中数学 来源： 题型：
【题目】锐角△ABC中，角A，B，C的对边分别为a，b，c，向量 
， 
，且 
．
（1）求角B的大小；
（2）若sinAsinC=sin2B，求a﹣c的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列选项中，说法正确的是（ ）
A.若a＞b＞0，则 
B.向量 
（m∈R）共线的充要条件是m=0
C.命题“?n∈N* ， 3n＞（n+2）?2n﹣1”的否定是“?n∈N* ， 3n≥（n+2）?2n﹣1”
D.已知函数f（x）在区间[a，b]上的图象是连续不断的，则命题“若f（a）?f（b）＜0，则f（x）在区间（a，b）内至少有一个零点”的逆命题为假命题
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱柱ABC﹣A1B1C1中，B1B=B1A=AB=BC，∠B1BC=90°，D为AC的中点，AB⊥B1D．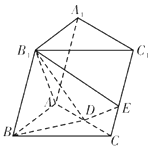 
（1）求证：平面ABB1A1⊥平面ABC；
（2）在线段CC1（不含端点）上，是否存在点E，使得二面角E﹣B1D﹣B的余弦值为 
？若存在，求出 
的值，若不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】现有7名学科竞赛优胜者，其中语文学科是A1 ， A2 ， 数学学科是B1 ， B2 ， 英语学科是C1 ， C2 ， 物理学科是D1 ， 从竞赛优胜者中选出3名组成一个代表队，要求每个学科至多选出1名．
（1）求B1被选中的概率；
（2）求代表队中有物理优胜者的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知命题p：k2﹣8k﹣20≤0，命题q：方程 
=1表示焦点在x轴上的双曲线． （Ⅰ）命题q为真命题，求实数k的取值范围；
（Ⅱ）若命题“p∨q”为真，命题“p∧q”为假，求实数k的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了检测某种产品的质量（单位：千克），抽取了一个容量为N的样本，整理得到的数据作出了频率分布表和频率分布直方图如图：
分组 | 频数 | 频率 |
[17.5，20） | 10 | 0.05 |
[20，225） | 50 | 0.25 |
[22.5，25） | a | b |
[25，27.5） | 40 | c |
[27.5，30] | 20 | 0.10 |
合计 | N | 1 |
（Ⅰ）求出表中N及a，b，c的值；
（Ⅱ）求频率分布直方图中d的值；
（Ⅲ）从该产品中随机抽取一件，试估计这件产品的质量少于25千克的概率．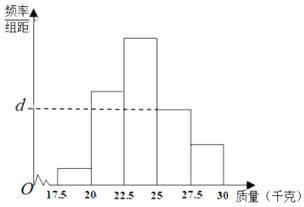
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
