
| A. | 2n-3 | B. | 2n-4 | C. | n-3 | D. | n-4 |
分析 先根据数列的递推公式得到(Sn-2Sn-1)2=SnSn-1,即可得到$\frac{{S}_{n}}{{S}_{n-1}}$+$\frac{4{S}_{n-1}}{{S}_{n}}$=5,解得Sn=4Sn-1,即可求出数列an的通项公式,再根据对数的运算性质即可求出答案.
解答 解:∵an=Sn-Sn-1,$({a}_{n}-{S}_{n-1})^{2}={S}_{n}{S}_{n-1}$,
∴(Sn-2Sn-1)2=SnSn-1,
∴Sn2+4Sn-12=5SnSn-1,
∴$\frac{{S}_{n}}{{S}_{n-1}}$+$\frac{4{S}_{n-1}}{{S}_{n}}$=5,
令$\frac{{S}_{n}}{{S}_{n-1}}$=t,
∴t+$\frac{4}{t}$=5,
解得t=1或t=4,
∴Sn=Sn-1,或Sn=4Sn-1,
∵正项数列{an}的前n项和为Sn,
∴Sn≠Sn-1,
∴Sn=4Sn-1,
∵S1=a1=1,
∴{Sn}是以1为首项,以4为公比的等比数列,
∴Sn=4n-1,
当n=1时,S1=a1=1,
当n≥2时,an+1=Sn+1-Sn=4n-4n-1=3×4n-1,
∴$\frac{{a}_{n+1}}{6}$=$\frac{3×{4}^{n-1}}{6}$=22n-3,
∴bn=log2$\frac{{a}_{n+1}}{6}$=2n-3,
故选:A.
点评 本题考查了数列的递推公式求出数列的通项公式以及等比数列的性质,考查了学生的运算能力,转化能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 有3个 | B. | 有2个 | C. | 有且只有1个 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
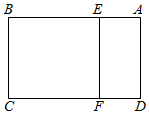 如图,在矩形ABCD中,AD=$\sqrt{5}$,AB=3,E、F分别为AB边、CD边上一点,且AE=DF=l,现将矩形ABCD沿EF折起,使得平面ADFE⊥平面BCFE,连接AB、CD,则所得三棱柱ABE-DCF的侧面积比原矩形ABCD的面积大约多(取$\sqrt{5}$≈2.236)( )
如图,在矩形ABCD中,AD=$\sqrt{5}$,AB=3,E、F分别为AB边、CD边上一点,且AE=DF=l,现将矩形ABCD沿EF折起,使得平面ADFE⊥平面BCFE,连接AB、CD,则所得三棱柱ABE-DCF的侧面积比原矩形ABCD的面积大约多(取$\sqrt{5}$≈2.236)( )| A. | 68% | B. | 70% | C. | 72% | D. | 75% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某程序框图如图所示,若输入输出的n分别为3和1,则在图中空白的判断框中应填入的条件可以为( )
某程序框图如图所示,若输入输出的n分别为3和1,则在图中空白的判断框中应填入的条件可以为( )| A. | i≥7? | B. | i>7? | C. | i≥6? | D. | i<6? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $2\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 0 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(6,±6\sqrt{2})$ | B. | $(6\sqrt{2},±6)$ | C. | $(12,±6\sqrt{2})$ | D. | $(6\sqrt{2},±12)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com