
| A. | (-∞,-1] | B. | $(-∞,-\frac{7}{2}]$ | C. | $[-\frac{7}{2},-1)$ | D. | $[-\frac{7}{2},+∞)$ |
分析 根据题意,已知f(x)在区间[2,+∞)上是减函数,即f′(x)=2x+a-$\frac{1}{x}$≤0在区间[2,+∞)上恒成立,对于恒成立往往是把字母变量放在一边即参变量分离,另一边转化为求函数在定义域下的最值,即可求解.
解答 解:f′(x)=2x+a-$\frac{1}{x}$,
∵函数f(x)在[1,2]上是减函数,
∴当x∈[1,2]时,f′(x)=2x+a-$\frac{1}{x}$≤0恒成立,即a≤-2x+$\frac{1}{x}$恒成立.
由于y=-2x+$\frac{1}{x}$在[1,2]上为减函数,
则ymin=-$\frac{7}{2}$,则a≤ymin=-$\frac{7}{2}$,
故选:B.
点评 本题主要考查了根据函数单调性求参数范围的问题,解题的关键将题目转化成f′(x)≤0在区间[1,2]上恒成立进行求解,同时考查了参数分离法,属于中档题.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 家庭类型 | 贫困 | 温饱 | 小康 | 富裕 |
| n | n≥59% | 50%≤n≤59% | 40%≤n≤50% | 30%≤n≤40% |
| A. | 贫困 | B. | 温饱 | C. | 小康 | D. | 富裕 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2<x<1} | B. | {x|-2<x<1或x>2} | C. | {x|x>2} | D. | {x|1<x<2或x<-2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
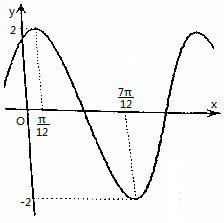 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一个周期内的图象如图.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一个周期内的图象如图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com