
已知集合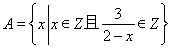 ,则集合
,则集合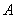 中的元素个数为( )
中的元素个数为( )
A.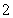 B.
B.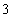 C.
C.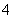 D.
D.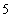
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:解答题
一个袋中装有若干个大小相同的黑球、白球和红球,已知从袋中任意摸出1个球,得到黑球的概率是 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是 .
.
(1)若袋中共有10个球,
①求白球的个数;
②从袋中任意摸出3个球,记得到白球的个数为X,求随机变量X的分布列.
(2)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于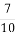 ,并指出袋中哪种颜色的球的个数最少.
,并指出袋中哪种颜色的球的个数最少.
查看答案和解析>>
科目:高中数学 来源:2014年陕西省咸阳市高考模拟考试(一)理科数学试卷(解析版) 题型:填空题
已知函数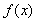 =x+sinx.项数为19的等差数列
=x+sinx.项数为19的等差数列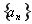 满足
满足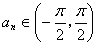 ,且公差
,且公差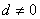 .若
.若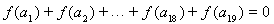 ,则当
,则当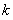 =__________时,
=__________时,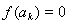 .
.
查看答案和解析>>
科目:高中数学 来源:2014年广东省广州市毕业班综合测试一理科数学试卷(解析版) 题型:解答题
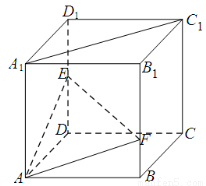
如图,在棱长为 的正方体
的正方体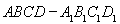 中,点
中,点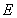 是棱
是棱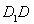 的中点,点
的中点,点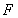 在棱
在棱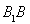 上,且满足
上,且满足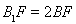 .
.
(1)求证: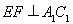 ;
;
(2)在棱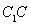 上确定一点
上确定一点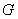 ,使
,使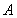 、
、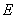 、
、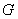 、
、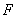 四点共面,并求此时
四点共面,并求此时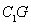 的长;
的长;
(3)求平面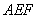 与平面
与平面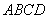 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2014年广东省广州市毕业班综合测试一文科数学试卷(解析版) 题型:填空题
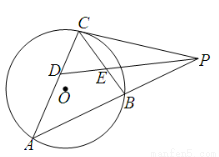
如图,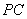 是圆
是圆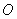 的切线,切点为点
的切线,切点为点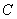 ,直线
,直线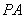 与圆
与圆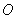 交于
交于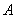 、
、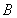 两点,
两点,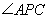 的角平分线交弦
的角平分线交弦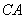 、
、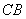 于
于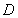 、
、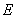 两点,已知
两点,已知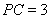 ,
,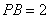 ,则
,则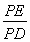 的值为 .
的值为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷2练习卷(解析版) 题型:解答题
已知公差不为0的等差数列{an},a1=1,且a2,a4-2,a6成等比数列.
(1)求数列{an}的通项公式;
(2)已知数列{bn}的通项公式是bn=2n-1,集合A={a1,a2,…,an,…},B={b1,b2,b3,…,bn,…}.将集合A∩B中的元素按从小到大的顺序排成一个新的数列{cn},求数列{cn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷6练习卷(解析版) 题型:解答题
甲、乙两所学校高三年级分别有1 200人,1 000人,为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下:
甲校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 3 | 4 | 8 | 15 |
|
|
|
|
|
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 15 | x | 3 | 2 |
乙校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 1 | 2 | 8 | 9 |
|
|
|
|
|
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 10 | 10 | y | 3 |
(1)计算x,y的值;
(2)若规定考试成绩在[120,150]内为优秀,请分别估计两所学校数学成绩的优秀率;
(3)由以上统计数据填写下面的2×2列联表,并判断能否在犯错误的概率不超过0.10的前提下认为两所学校的数学成绩有差异.
| 甲校 | 乙校 | 总计 |
优秀 |
|
|
|
非优秀 |
|
|
|
总计 |
|
|
|
参考数据与公式:由列联表中数据计算K2=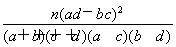 . ?
. ?
临界值表
P(K2≥k0) | 0.10 | 0.05 | 0.010 |
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com