
【题目】设函数f(x)=|3x﹣1|+ax+3,a∈R.
(1)若a=1,解不等式f(x)≤4;
(2)若函数f(x)有最小值,求a的取值范围.
【答案】
(1)解:当a=1时,f(x)=|3x﹣1|+x+3;
①当 ![]() 时,f(x)≤4可化为3x﹣1+x+3≤4,解得
时,f(x)≤4可化为3x﹣1+x+3≤4,解得 ![]() ;
;
②当 ![]() 时,f(x)≤4可化为﹣3x+1+x+3≤4,解得
时,f(x)≤4可化为﹣3x+1+x+3≤4,解得 ![]() ;
;
综上可得,原不等式的解集为 ![]()
(2)解:  ;
;
函数f(x)有最小值的充要条件为 ![]() ;
;
即﹣3≤a≤3;
∴a的取值范围为[﹣3,3]
【解析】(1)a=1时,得出f(x)=|3x﹣1|+x+3,这样可讨论x,从而去绝对值号即可将f(x)≤4转化为关于x的一元一次不等式,解不等式得出x的范围,求并集即得出原不等式的解集;(2)去绝对值号便可得出  ,这样便可看出,要使得f(x)有最小值,需满足
,这样便可看出,要使得f(x)有最小值,需满足 ![]() ,这样便可得出a的取值范围.
,这样便可得出a的取值范围.
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() (其中a>0,且a≠1).
(其中a>0,且a≠1).
(1)请你推测g(5)能否用f(2),f(3),g(2),g(3)来表示;
(2)如果(1)中获得了一个结论,请你推测能否将其推广.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为![]() .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为![]() 时,求k的值.
时,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若正整数N除以正整数m后的余数为n,则记为N≡n(mod m),例如10≡4(mod 6).下面程序框图的算法源于我国古代闻名中外的(中国剩余定理),执行该程序框图,则输出的n等于( ) 
A.17
B.16
C.15
D.13
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆 ![]() =1(a>b>0)的左、右顶点分别为A,B,焦距为2
=1(a>b>0)的左、右顶点分别为A,B,焦距为2 ![]() ,直线x=﹣a与y=b交于点D,且|BD|=3
,直线x=﹣a与y=b交于点D,且|BD|=3 ![]() ,过点B作直线l交直线x=﹣a于点M,交椭圆于另一点P.
,过点B作直线l交直线x=﹣a于点M,交椭圆于另一点P. 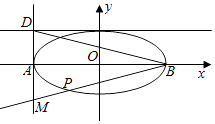
(1)求椭圆的方程;
(2)证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣a(x﹣1),g(x)=ex .
(1)当a=2时,求函数f(x)的最值;
(2)当a≠0时,过原点分别作曲线y=f(x)与y=g(x)的切线l1 , l2 , 已知两切线的斜率互为倒数,证明: ![]() <a<
<a< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,其可见部分如图所示.据此解答如下问题:
(1)计算频率分布直方图中[80,90)间的矩形的高;
(2)根据茎叶图和频率分布直方图估计这次测试的平均分.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com