
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | c<a<b |
分析 根据零点存在定理,分别求三个函数的零点,判断零点的范围,再判断函数的单调性,确定函数的零点的唯一性,从而得到结果.
解答 解:函数f(x)=2x+x,f(-1)=$\frac{1}{2}$-1=-$\frac{1}{2}$<0,f(0)=1>0,可知函数的零点a<0;
令g(x)=x-3=0得,b=3;
函数h(x)=log2x+x=0,h($\frac{1}{2}$)=-1+$\frac{1}{2}$=-$\frac{1}{2}$<0,h(1)=1>0,
∴函数的零点满足$\frac{1}{2}$<c<1,
∵f(x)=2x+x,g(x)=x-3,h(x)=log2x+x在定义域上是增函数,
∴函数的零点是唯一的,
则a<c<b,
故选:B.
点评 本题考查的重点是函数的零点及个数的判断,基本初等函数的单调性的应用,解题的关键是利用零点存在定理,确定零点的值或范围.


科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=$\frac{1}{8}$x | B. | y2=2x | C. | y=2x2 | D. | y=$\frac{1}{2}$x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈(-∞,0),x3+2x<0 | B. | ?x∈[0,+∞),x3+2x<0 | C. | ?x∈(-∞,0),x3+2x≥0 | D. | ?x∈[0,+∞),x3+2x≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .1 | B. | .2 | C. | .3 | D. | .4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (cosx)′=sinx | B. | (ax)′=axlna | C. | ${({sin\frac{π}{12}})^'}=cos\frac{π}{12}$ | D. | ${({{x^{-5}}})^'}=-\frac{1}{5}{x^{-6}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
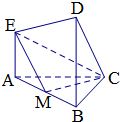 在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE,M是AB的中点.
在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE,M是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com