练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     

    平面内有向量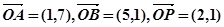，点M为直线OP上的一个动点．

    （1）当取得最小值时，求点M的坐标；

    （2）在点M满足（1）的条件下，求的余弦值．

     

    【答案】

    （1）－8，          ……………… 6分

     (2)                        ……………… 12分

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：学习周报　数学　北师大课标高一版(必修4)　2009－2010学年　第47期　总203期 北师大课标版 题型：044

    平面内有向量＝(1，7)，＝(5，1)，＝(2，1)，点M为直线OP上的一个动点．

    (1)当·取最小值时，求的坐标；

    (2)当点M满足(1)的条件和结论时，求cos∠AMB的值．

    查看答案和解析>>

    科目：高中数学 来源：山东省汶上一中2010－2011学年高一下学期期末考试数学试题 题型：044

    平面内有向量＝(1，7)，＝(5，1)，＝(2，1)，点M为直线OP上的一个动点．

    (1)当·取得最小值时，求点M的坐标；

    (2)在点M满足(1)的条件下，求∠AMB的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，平面内有向量=(1，7)，=?(5，1)，=(2，1)，点M为直线OP上的一动点.

    (1)当取最小值时，求的坐标；

    (2)当点M满足(1)的条件和结论时，求∠AMB的值.

    查看答案和解析>>

    科目：高中数学 来源：0115 期末题 题型：解答题

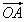    平面内有向量=（1，7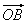），=（5，1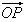），=（2，1），点M为直线OP上的一个动点，
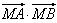    （1）当取得最小值时，求点M的坐标；
    （2）在点M满足（1）的条件下，求∠AMB的余弦值。

    查看答案和解析>>

    同步练习册答案