练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，矩形ABCD的两条对角线相交于点M(2,0)，AB边所在直线的方程为x－3y－6＝0，点T(－1,1)在AD边所在的直线上．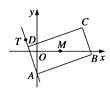

    （1）求AD边所在直线的方程；
    （2）求矩形ABCD外接圆的方程．

    【答案】
    （1）解：因为AB边所在直线的方程为x－3y－6＝0，且AD与AB垂直，所以直线AD的斜率为－3.又因为点T(－1,1)在直线AD上，所以AD边所在直线的方程为y－1＝－3(x＋1)，即3x＋y＋2＝0
    （2）解：由 可得点A的坐标为(0，－2)．
    因为矩形ABCD两条对角线的交点为M(2,0)．
    所以M为矩形ABCD外接圆的圆心．又|AM|＝ ，
    从而矩形ABCD外接圆的方程为(x－2)2＋y2＝8
    【解析】本题考查直线方程的求法，考查圆的方程的求法，考查向量数量积的求法，解题时要认真审题，注意直线性质的灵活运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图所示，一个圆锥形的空杯子上放着一个直径为8cm的半球形的冰淇淋，请你设计一种这样的圆锥形杯子（杯口直径等于半球形的冰淇淋的直径，杯子壁厚忽略不计），使冰淇淋融化后不会溢出杯子，怎样设计最省材料？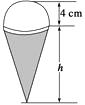

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一枚硬币连续掷三次，至少出现一次正面朝上的概率为( )
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= ，则y=f（x）的图象大致为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】己知（2x﹣ ）5（Ⅰ）求展开式中含 项的系数
    （Ⅱ）设（2x﹣ ）5的展开式中前三项的二项式系数之和为M，（1+ax）6的展开式中各项系数之和为N，若4M=N，求实数a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】直线l1过点A(0,1)，l2过点B(5,0)，如果l1∥l2且l1与l2的距离为5，求l1 ， l2的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知N为自然数集，集合P＝{1,4,7,10,13}，Q＝{2,4,6,8,10}，则P∩ 等于（ ）
    A.{1,7,13}
    B.{4,10}
    C.{1,7}
    D.{0,1,3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ．
    （1）若曲线y=f（x）在P（1，f（1））处的切线平行于直线y=﹣x+1，求函数y=f（x）的单调区间；
    （2）若a＞0，且对任意x∈（0，2e]时，f（x）＞0恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角梯形ABCD中，AB⊥AD，AD∥BC，AB=BC=2AD=2，E，F分别为BC，CD的中点，以A为圆心，AD为半径的圆交AB于G，点P在 上运动（如图）．若 =λ +μ ，其中λ，μ∈R，则6λ+μ的取值范围是（ ）
    A.[1， ]
    B.[ ，2 ]
    C.[2，2 ]
    D.[1，2 ]

    查看答案和解析>>

    同步练习册答案