
【题目】已知函数f(x)=ax3+|x-a|,a![]() R.
R.
(1)若a=-1,求函数y=f(x) (x![]() [0,+∞))的图象在x=1处的切线方程;
[0,+∞))的图象在x=1处的切线方程;
(2)若g(x)=x4,试讨论方程f(x)=g(x)的实数解的个数;
(3)当a>0时,若对于任意的x1![]() [a,a+2],都存在x2
[a,a+2],都存在x2![]() [a+2,+∞),使得f(x1)f(x2)=1024,求满足条件的正整数a的取值的集合.
[a+2,+∞),使得f(x1)f(x2)=1024,求满足条件的正整数a的取值的集合.
【答案】(1)2x+y-3=0.(2)当a≥1时,方程f(x)=g(x)有两个不同的解a,-1;当-1<a<1时,方程f(x)=g(x)有三个不同的解a,-1,1;当a≤-1时,方程f(x)=g(x)有两个不同的解a,1.(3){1}.
【解析】试题分析:(1)当a=-1,x![]() [0,+∞)时,f(x)=-x3+x+1,从而f ′(x)=-3x2+1.当x=1时,f(1)=1,f ′(1)=-2,所以函数y=f(x) (x
[0,+∞)时,f(x)=-x3+x+1,从而f ′(x)=-3x2+1.当x=1时,f(1)=1,f ′(1)=-2,所以函数y=f(x) (x![]() [0,+∞))的图象在x=1处的切线方程为y-1=-2(x-1),即2x+y-3=0.(2)本题第一个难点在于化简方程,提取公因式;第二个难点,在于讨论三个条件关系. f(x)=g(x)即为ax3+|x-a|=x4.所以x4-ax3=|x-a|,从而x3(x-a)=|x-a|.此方程等价于x=a或
[0,+∞))的图象在x=1处的切线方程为y-1=-2(x-1),即2x+y-3=0.(2)本题第一个难点在于化简方程,提取公因式;第二个难点,在于讨论三个条件关系. f(x)=g(x)即为ax3+|x-a|=x4.所以x4-ax3=|x-a|,从而x3(x-a)=|x-a|.此方程等价于x=a或![]() 或
或![]() 所以当a≥1时,方程f(x)=g(x)有两个不同的解a,-1;当-1<a<1时,方程f(x)=g(x)有三个不同的解a,-1,1;当a≤-1时,方程f(x)=g(x)有两个不同的解a,1.(3)对条件的转化是本题难点,本题从函数值域包含关系出发.易得函数f(x)在(a,+∞)上是增函数,
所以当a≥1时,方程f(x)=g(x)有两个不同的解a,-1;当-1<a<1时,方程f(x)=g(x)有三个不同的解a,-1,1;当a≤-1时,方程f(x)=g(x)有两个不同的解a,1.(3)对条件的转化是本题难点,本题从函数值域包含关系出发.易得函数f(x)在(a,+∞)上是增函数, 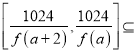 [ f(a+2),+∞).从而
[ f(a+2),+∞).从而![]() ≥f(a+2).所以f2(a+2)≤1024,即f(a+2)≤32,也即a(a+2)3+2≤32.因为a>0,显然a=1满足,而a≥2时,均不满足.所以满足条件的正整数a的取值的集合为{1}.
≥f(a+2).所以f2(a+2)≤1024,即f(a+2)≤32,也即a(a+2)3+2≤32.因为a>0,显然a=1满足,而a≥2时,均不满足.所以满足条件的正整数a的取值的集合为{1}.
试题解析:解:(1)当a=-1,x![]() [0,+∞)时,f(x)=-x3+x+1,从而f ′(x)=-3x2+1.
[0,+∞)时,f(x)=-x3+x+1,从而f ′(x)=-3x2+1.
当x=1时,f(1)=1,f ′(1)=-2,
所以函数y=f(x) (x![]() [0,+∞))的图象在x=1处的切线方程为y-1=-2(x-1),
[0,+∞))的图象在x=1处的切线方程为y-1=-2(x-1),
即2x+y-3=0. 3分
(2)f(x)=g(x)即为ax3+|x-a|=x4.
所以x4-ax3=|x-a|,从而x3(x-a)=|x-a|.
此方程等价于x=a或或
![]() 6分
6分
所以当a≥1时,方程f(x)=g(x)有两个不同的解a,-1;
当-1<a<1时,方程f(x)=g(x)有三个不同的解a,-1,1;
当a≤-1时,方程f(x)=g(x)有两个不同的解a,1. 9分
(3)当a>0,x![]() (a,+∞)时,f(x)=ax3+x-a,f ′(x)=3ax2+1>0,
(a,+∞)时,f(x)=ax3+x-a,f ′(x)=3ax2+1>0,
所以函数f(x)在(a,+∞)上是增函数,且f(x)>f(a)=a4>0.
所以当x![]() [a,a+2]时,f(x)
[a,a+2]时,f(x) ![]() [f(a),f(a+2)],
[f(a),f(a+2)], 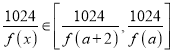 ,
,
当x![]() [a+2,+∞)时,f(x)
[a+2,+∞)时,f(x) ![]() [ f(a+2),+∞). 11分
[ f(a+2),+∞). 11分
因为对任意的x1![]() [a,a+2],都存在x2
[a,a+2],都存在x2![]() [a+2,+∞),使得f(x1)f(x2)=1024,
[a+2,+∞),使得f(x1)f(x2)=1024,
所以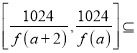 [ f(a+2),+∞). 13分
[ f(a+2),+∞). 13分
从而![]() ≥f(a+2).
≥f(a+2).
所以f2(a+2)≤1024,即f(a+2)≤32,也即a(a+2)3+2≤32.
因为a>0,显然a=1满足,而a≥2时,均不满足.
所以满足条件的正整数a的取值的集合为{1}. 16分


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,点A,B的坐标分别是(0,﹣3),(0,3)直线AM,BM相交于点M,且它们的斜率之积是﹣![]() .
.
(1)求点M的轨迹L的方程;
(2)若直线L经过点P(4,1),与轨迹L有且仅有一个公共点,求直线L的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() 的极值点.
的极值点.
(1)若函数f(x)在x=2的切线平行于3x﹣4y+4=0,求函数f(x)的解析式;
(2)若f(x)=0恰有两解,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosα,sinα)(0≤α<2π),
=(cosα,sinα)(0≤α<2π), ![]() =(﹣
=(﹣ ![]() ,
, ![]() ).
).
(1)若 ![]() ∥
∥ ![]() ,求α的值;
,求α的值;
(2)若两个向量 ![]() +
+ ![]() 与
与 ![]() ﹣
﹣ ![]() 垂直,求tanα.
垂直,求tanα.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(示意),公路AM、AN围成的是一块顶角为α的角形耕地,其中tanα=-2.在该块土地中P处有一小型建筑,经测量,它到公路AM,AN的距离分别为3km,km.现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园.为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.
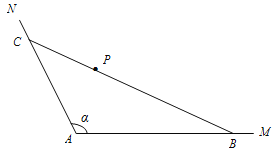
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是单调递增的等差数列,首项a1=3,前n项和为Sn , 数列{bn}是等比数列,首项b1=1,且a2b2=12,S3+b2=20.
(1)求{an}和{bn}的通项公式.
(2)令Cn=nbn(n∈N+),求{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤ ![]() )的图象与坐标轴的三个交点为P,Q,R,且P(1,0),Q(m,0)(m>0),∠PQR=
)的图象与坐标轴的三个交点为P,Q,R,且P(1,0),Q(m,0)(m>0),∠PQR= ![]() ,M为QR的中点,|PM|=
,M为QR的中点,|PM|= ![]() .
. 
(1)求m的值及f(x)的解析式;
(2)设∠PRQ=θ,求tanθ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com