
 ,∠BAC=30°,若它们的斜边AB重合,让三角板ABD以AB为轴转动,则下列说法正确的是 .
,∠BAC=30°,若它们的斜边AB重合,让三角板ABD以AB为轴转动,则下列说法正确的是 .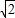 ;
;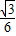 .
.
 解:①取AB中点O,连接DO、CO,
解:①取AB中点O,连接DO、CO, ,∴DO=1,AB=2,OC=1
,∴DO=1,AB=2,OC=1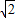 ,①正确;
,①正确; ×
× ×AC×BC×DO=
×AC×BC×DO= ×
× ×1×1=
×1×1=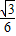 .③正确.
.③正确. Sh.
Sh. 

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
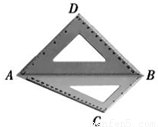
 将一幅斜边长相等的直角三角板拼接成如图所示的空间图形,其中AD=BD=
将一幅斜边长相等的直角三角板拼接成如图所示的空间图形,其中AD=BD=| 2 |
| 2 |
| ||
| 6 |
查看答案和解析>>
科目:高中数学 来源:2015届福建省高一上学期期末考试数学试卷(解析版) 题型:填空题
将一幅斜边长相等的直角三角板拼接成如图所示的空间图形,其中AD=BD=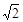 ,∠BAC=30°,若它们的斜边AB重合,让三角板ABD以AB为轴转动,则下列说法正确的是 .
,∠BAC=30°,若它们的斜边AB重合,让三角板ABD以AB为轴转动,则下列说法正确的是 .
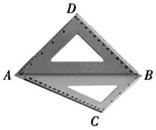
①当平面ABD⊥平面ABC时,C、D两点间的距离为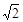 ;
;
②在三角板ABD转动过程中,总有AB⊥CD;
③在三角板ABD转动过程中,三棱锥D-ABC体积的最大值为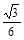 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 将一幅斜边长相等的直角三角板拼接成如图所示的空间图形,其中AD=BD=
将一幅斜边长相等的直角三角板拼接成如图所示的空间图形,其中AD=BD= ,∠BAC=30°,若它们的斜边AB重合,让三角板ABD以AB为轴转动,则下列说法正确的是________.
,∠BAC=30°,若它们的斜边AB重合,让三角板ABD以AB为轴转动,则下列说法正确的是________. ;
; .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com