
【题目】已知![]() ,
,![]() 是双曲线
是双曲线![]() 的左、右焦点,点P为
的左、右焦点,点P为![]() 上异于顶点的点,直线l分别与以
上异于顶点的点,直线l分别与以![]() ,
,![]() 为直径的圆相切于A,B两点,若向量
为直径的圆相切于A,B两点,若向量![]() ,
,![]() 的夹角为
的夹角为![]() ,则
,则![]() =___________.
=___________.
【答案】![]()
【解析】
首先将图象画出来,设以PF1,PF2为直径的圆的圆心分别为C,D,连接AC,BD,过D作DE⊥AC于点E,连接CD,易证四边形ABDE是矩形,根据几何关系可得|CE|==![]() =5,由
=5,由![]() 可得
可得![]() ,又向量
,又向量![]() 的夹角
的夹角![]() 即为
即为![]() 的夹角,从而
的夹角,从而![]() .
.
如图,设以PF1,PF2为直径的圆的圆心分别为C,D,连接AC,BD,

过D作DE⊥AC于点E,连接CD,则![]() ,
,
因为直线AB是圆C和圆D的公切线,且切点分别是A,B,
所以AC⊥AB,BD⊥AB,则四边形ABDE是矩形,所以|AB|=|DE|,|AE|=|BD|.
且![]() ,
,![]() ,易知|CE|=|AC|-|AE|=|AC|-|BD|=
,易知|CE|=|AC|-|AE|=|AC|-|BD|=![]() ,
,
根据双曲线的定义知,|PF1|-|PF2|=10,所以|CE|=5.
因为![]() ,由
,由![]() |可得
|可得![]() ,
,
即|AB|=3,因为向量![]() 的夹角
的夹角![]() 即为
即为![]() 的夹角,
的夹角,
所以![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 是
是![]() 上一点.
上一点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是
是![]() 分别关于两坐标轴及坐标原点的对称点,平行于
分别关于两坐标轴及坐标原点的对称点,平行于![]() 的直线
的直线![]() 交
交![]() 于异于
于异于![]() 的两点
的两点![]() .点
.点![]() 关于原点的对称点为
关于原点的对称点为![]() .证明:直线
.证明:直线![]() 与
与![]() 轴围成的三角形是等腰三角形.
轴围成的三角形是等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的图象的一个最高点为(![]() ),与之相邻的一个对称中心为
),与之相邻的一个对称中心为![]() ,将f(x)的图象向右平移
,将f(x)的图象向右平移![]() 个单位长度得到函数g(x)的图象,则( )
个单位长度得到函数g(x)的图象,则( )
A.g(x)为偶函数
B.g(x)的一个单调递增区间为![]()
C.g(x)为奇函数
D.函数g(x)在![]() 上有两个零点
上有两个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为提高产品质量,某企业质量管理部门经常不定期地对产品进行抽查检测,现对某条生产线上随机抽取的100个产品进行相关数据的对比,并对每个产品进行综合评分(满分100分),将每个产品所得的综合评分制成如图所示的频率分布直方图.记综合评分为80分及以上的产品为一等品.
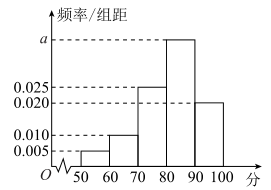
(1)求图中![]() 的值,并求综合评分的中位数;
的值,并求综合评分的中位数;
(2)用样本估计总体,视频率作为概率,在该条生产线中随机抽取3个产品,求所抽取的产品中一等品数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
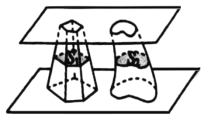
【题目】南北朝时代的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”.其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平行平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等,如图,夹在两个平行平面之间的两个几何体的体积分别为![]() ,
,![]() ,被平行于这两个平面的任意平面截得的两个截面面积分别为
,被平行于这两个平面的任意平面截得的两个截面面积分别为![]() 、
、![]() ,则“
,则“![]() 、
、![]() 不总相等”是“
不总相等”是“![]() ,
,![]() 不相等”的( )
不相等”的( )
A.充分而不必要条件B.必要而不充分条件
C.充分必要条件D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线C:
中,抛物线C:![]() (
(![]() )的焦点为
)的焦点为![]()
(1)动直线l过F点且与抛物线C交于M,N两点,点M在y轴的左侧,过点M作抛物线C准线的垂线,垂足为M1,点E在![]() 上,且满足
上,且满足![]()
![]() 连接
连接![]() 并延长交y轴于点D,
并延长交y轴于点D,![]() 的面积为
的面积为![]() ,求抛物线C的方程及D点的纵坐标;
,求抛物线C的方程及D点的纵坐标;
(2)点H为抛物线C准线上任一点,过H作抛物线C的两条切线![]() ,
,![]() ,切点为A,B,证明直线
,切点为A,B,证明直线![]() 过定点,并求
过定点,并求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com