练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知三棱柱ABC﹣A1B1C1的侧棱垂直于底面，且其6个顶点都在球O的球面上，若AB=3，AC=4，AB⊥AC，AA1=12，则球O的半径为 ．

    【答案】
    【解析】解：因为三棱柱ABC﹣A1B1C1的6个顶点都在球O的球面上，若AB=3，AC=4，AB⊥AC，AA1=12，
    所以三棱柱的底面是直角三角形，侧棱与底面垂直，侧面B1BCC1 ， 经过球的球心，球的直径是其对角线的长，
    因为AB=3，AC=4，BC=5，BC1= =13．
    所以球的半径为： ．
    所以答案是： ．

    【考点精析】根据题目的已知条件，利用球内接多面体的相关知识可以得到问题的答案，需要掌握球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设 ．若f（x）=x2+px+q的图象经过两点（α，0），（β，0），且存在整数n，使得n＜α＜β＜n+1成立，则（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线： 的焦点为，圆： .直线与抛物线交于点、两点，与圆切于点.

    （1）当切点的坐标为时，求直线及圆的方程；

    （2）当时，证明： 是定值，并求出该定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=Asin（ωx+φ）（ω＞0，0＜φ＜ ）的部分图象如图．

    （1）求f（x）的解析式；
    （2）将函数y=f（x）的图象上所有点的纵坐标不变，横坐标缩短为原来的 倍，再将所得函数图象向右平移 个单位，得到函数y=g（x）的图象，求g（x）的单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市上年度电价为0.80元/千瓦时，年用电量为a千瓦时．本年度计划将电价降到0.55元/千瓦时～0.75元/千瓦时之间，而居民用户期望电价为0.40元/千瓦时（该市电力成本价为0.30元/千瓦时）经测算，下调电价后，该城市新增用电量与实际电价和用户期望电价之差成反比，比例系数为0.2a．试问当地电价最低为多少时，可保证电力部门的收益比上年度至少增加20%．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，AB是圆O的直径，PA⊥圆O所在的平面，C是圆O上的点．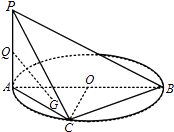

    （1）求证：BC⊥平面PAC；
    （2）若Q为PA的中点，G为△AOC的重心，求证：QG∥平面PBC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某网站针对2014年中国好声音歌手A，B，C三人进行网上投票，结果如下：

    观众年龄

    支持A

    支持B

    支持C

    20岁以下

    200

    400

    800

    20岁以上（含20岁）

    100

    100

    400

    （1）在所有参与该活动的人中，用分层抽样的方法抽取n人，其中有6人支持A，求n的值．
    （2）在支持C的人中，用分层抽样的方法抽取6人作为一个总体，从这6人中任意选取2人，求恰有1人在20岁以下的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知α，β为锐角， =cos（α+β）．
    （1）求tan（α+β）cotα的值；
    （2）求tanβ的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，内角A、B、C的对边分别是a、b、c，且b2+c2﹣a2=bc．
    （1）求A；
    （2）若a= ，sinBsinC=sin2A，求△ABC的周长．

    查看答案和解析>>

    同步练习册答案