
【题目】设函数f(x)=|x+1|﹣|2x﹣4|;
(1)解不等式f(x)≥1;
(2)若对x∈R,都有f(x)+3|x﹣2|>m,求实数m的取值范围.
【答案】
(1)解: f(x)=|x+1|﹣|2x﹣4|=|x+1|﹣2|x﹣2|≥1,
x≥2时,x+1﹣2x+4≥1,解得:x≤4,
﹣1<x<2时,x+1+2x﹣4≥1,解得:x≥ ![]() ,
,
x≤﹣1时,﹣x﹣1+2x﹣4≥1,无解,
故不等式的解集是[ ![]() ,4];
,4];
(2)解:若对x∈R,都有f(x)+3|x﹣2|>m,
即若对x∈R,都有|x+1|+|x﹣2|>m,
而|x+1|+|x﹣2|≥|x+1﹣x+2|=3,
故m<3.
【解析】(1)通过讨论x的范围,求出不等式的解集,取并集即可;(2)根据绝对值的性质求出f(x)+3|x﹣2|的最小值,从而求出m的范围即可.
【考点精析】利用绝对值不等式的解法对题目进行判断即可得到答案,需要熟知含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)当x∈(0,1)时,求f(x)的单调性;
(2)若h(x)=(x2﹣x)f(x),且方程h(x)=m有两个不相等的实数根x1 , x2 . 求证:x1+x2>1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着我国汽车消费水平的提高,二手车流通行业得到迅猛发展.某汽车交易市场对2017年成交的二手车交易前的使用时间(以下简称“使用时间”)进行统计,得到频率分布直方图如图1.


图1 图2
(1)记“在![]() 年成交的二手车中随机选取一辆,该车的使用年限在
年成交的二手车中随机选取一辆,该车的使用年限在![]() ”为事件
”为事件![]() ,试估计
,试估计![]() 的概率;
的概率;
(2)根据该汽车交易市场的历史资料,得到散点图如图2,其中![]() (单位:年)表示二手车的使用时间,
(单位:年)表示二手车的使用时间,![]() (单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用
(单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用![]() 作为二手车平均交易价格
作为二手车平均交易价格![]() 关于其使用年限
关于其使用年限![]() 的回归方程,相关数据如下表(表中
的回归方程,相关数据如下表(表中![]() ,
,![]() ):
):

①根据回归方程类型及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
②该汽车交易市场对使用8年以内(含8年)的二手车收取成交价格![]() 的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格
的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格![]() 的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
附注:①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;
②参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办![]() 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否在犯错误的概率不超过![]() 的前提下认为支持申办足球世界杯与性别有关;
的前提下认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退休老人中随机抽取
位退休老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司订购了一批树苗,为了检测这批树苗是否合格,从中随机抽测![]() 株树苗的高度,经数据处理得到如图的频率分布直方图,起中最高的
株树苗的高度,经数据处理得到如图的频率分布直方图,起中最高的![]() 株树苗高度的茎叶图如图所示,以这
株树苗高度的茎叶图如图所示,以这![]() 株树苗的高度的频率估计整批树苗高度的概率.
株树苗的高度的频率估计整批树苗高度的概率.

(1)求这批树苗的高度高于![]() 米的概率,并求图19-1中,
米的概率,并求图19-1中,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)若从这批树苗中随机选取![]() 株,记
株,记![]() 为高度在
为高度在![]() 的树苗数列,求
的树苗数列,求![]() 的分布列和数学期望.
的分布列和数学期望.
(3)若变量![]() 满足
满足![]() 且
且 ![]() ,则称变量
,则称变量![]() 满足近似于正态分布
满足近似于正态分布![]() 的概率分布.如果这批树苗的高度满足近似于正态分布
的概率分布.如果这批树苗的高度满足近似于正态分布![]() 的概率分布,则认为这批树苗是合格的,将顺利获得签收;否则,公司将拒绝签收.试问,该批树苗能否被签收?
的概率分布,则认为这批树苗是合格的,将顺利获得签收;否则,公司将拒绝签收.试问,该批树苗能否被签收?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线. 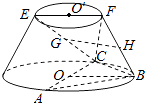
(1)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(2)已知EF=FB= ![]() AC=2
AC=2 ![]() ,AB=BC,求二面角F﹣BC﹣A的余弦值.
,AB=BC,求二面角F﹣BC﹣A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,分别是椭圆
,分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若点![]() 是第一象限内椭圆上的一点,
是第一象限内椭圆上的一点, ![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)设过定点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com