
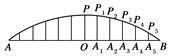
【题目】某圆拱桥的示意图如图所示,该圆拱的跨度AB是36 m,拱高OP是6 m,在建造时,每隔3 m需用一个支柱支撑,求支柱A2P2的长.(精确到0.01 m)
科目:高中数学 来源: 题型:
【题目】已知椭圆E的右焦点与抛物线y2=4x的焦点重合,点M ![]() 在椭圆E上. (Ⅰ)求椭圆E的标准方程;
在椭圆E上. (Ⅰ)求椭圆E的标准方程;
(Ⅱ)设P(﹣4,0),直线y=kx+1与椭圆E交于A,B两点,若∠APO=∠BPO,(其中O为坐标原点),
求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax+1(a∈R).
(1)若函数f(x)的图象在x=1处的切线l垂直于直线y=x,求实数a的值及直线l的方程;
(2)求函数f(x)的单调区间;
(3)若x>1,求证:lnx<x﹣1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于两条平行直线和圆的位置关系定义如下:若两直线中至少有一条与圆相切,则称该位置关系为“平行相切”;若两直线都与圆相离,则称该位置关系为“平行相离”;否则称为“平行相交”.已知直线l1:ax+3y+6=0,l2:2x+(a+1)y+6=0与圆C:x2+y2+2x=b2-1(b>0)的位置关系是“平行相交”,则实数b的取值范围为 ( )
A. (![]() ,
, ![]() ) B. (0,
) B. (0, ![]() )
)
C. (0, ![]() ) D. (
) D. (![]() ,
, ![]() )∪(
)∪(![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果函数f(x)在[a,b]上存在x1 , x2(a<x1<x2<b)满足 ![]() ,
, ![]() ,则称函数f(x)是[a,b]上的“双中值函数”.已知函数f(x)=x3﹣x2+a是[0,a]上的“双中值函数”,则实数a的取值范围是( )
,则称函数f(x)是[a,b]上的“双中值函数”.已知函数f(x)=x3﹣x2+a是[0,a]上的“双中值函数”,则实数a的取值范围是( )
A.![]()
B.( ![]() )
)
C.( ![]() ,1)
,1)
D.( ![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示的平面图形中,ABCD是边长为2的正方形,△HDA和△GDC都是以D为直角顶点的等腰直角三角形,点E是线段GC的中点.现将△HDA和△GDC分别沿着DA,DC翻折,直到点H和G重合为点P.连接PB,得如图2的四棱锥. 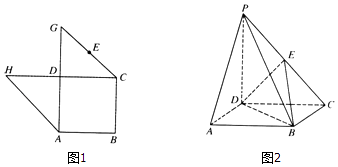
(Ⅰ)求证:PA∥平面EBD;
(Ⅱ)求二面角C﹣PB﹣D大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=xlnx,g(x)=﹣x2+ax﹣3.
(1)求函数f(x)在[t,t+2](t>0)上的最小值;
(2)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com