
【题目】某地出现了虫害,农业科学家引入了“虫害指数”数列![]() ,
,![]() 表示第
表示第![]() 周的虫害的严重程度,虫害指数越大,严重程度越高,为了治理虫害,需要环境整治、杀灭害虫,然而由于人力资源有限,每周只能采取以下两个策略之一:
周的虫害的严重程度,虫害指数越大,严重程度越高,为了治理虫害,需要环境整治、杀灭害虫,然而由于人力资源有限,每周只能采取以下两个策略之一:
策略![]() :环境整治,“虫害指数”数列满足
:环境整治,“虫害指数”数列满足![]() ;
;
策略![]() :杀灭害虫,“虫害指数”数列满足
:杀灭害虫,“虫害指数”数列满足![]() ;
;
当某周“虫害指数”小于1时,危机就在这周解除.
(1)设第一周的虫害指数![]() ,用哪一个策略将使第二周的虫害严重程度更小?
,用哪一个策略将使第二周的虫害严重程度更小?
(2)设第一周的虫害指数![]() ,如果每周都采用最优的策略,虫害的危机最快在第几周解除?
,如果每周都采用最优的策略,虫害的危机最快在第几周解除?
科目:高中数学 来源: 题型:
【题目】某数学教师在甲、乙两个平行班采用“传统教学”和“高效课堂”两种不同的教学模式进行教学实验.为了解教改实效,期中考试后,分别从两个班中各随机抽取![]() 名学生的数学成绩进行统计,得到如下的茎叶图:
名学生的数学成绩进行统计,得到如下的茎叶图:
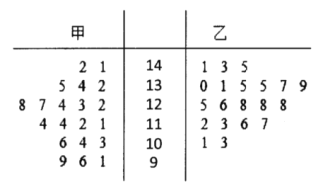
(Ⅰ)求甲、乙两班抽取的分数的中位数,并估计甲、乙两班数学的平均水平和分散程度(不要求计算出具体值,给出结论即可);
(Ⅱ)若规定分数在![]() 的为良好,现已从甲、乙两班成绩为良好的同学中,用分层抽样法抽出
的为良好,现已从甲、乙两班成绩为良好的同学中,用分层抽样法抽出![]() 位同学进行问卷调查,求这
位同学进行问卷调查,求这![]() 位同学中恰含甲、乙两班所有
位同学中恰含甲、乙两班所有![]() 分以上的同学的概率.
分以上的同学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为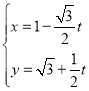 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,以x轴正半轴为极轴,建立极坐标系,曲线
为极点,以x轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 、
、![]() 为曲线
为曲线![]() 上位于第一,二象限的两个动点,且
上位于第一,二象限的两个动点,且![]() ,射线
,射线![]() ,
,![]() 交曲线
交曲线![]() 分别于点
分别于点![]() ,
,![]() .求
.求![]() 面积的最小值,并求此时四边形
面积的最小值,并求此时四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司招聘快递骑手,该公司提供了两种日工资方案:方案(1)规定每日底薪50元,快递骑手每完成一单业务提成3元:方案(2)规定每日底薪100元,快递业务的前44单没有提成,从第45单开始,每完成一单提成5元.该快递公司记录了每天骑手的人均业务量.现随机抽取100天的数据,将样本数据分为![]() 七组,整理得到如图所示的频率分布直方图.
七组,整理得到如图所示的频率分布直方图.
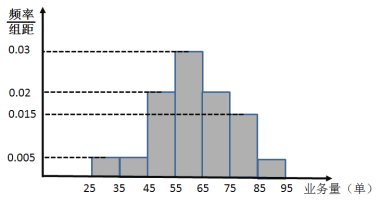
(Ⅰ)随机选取一天,估计这一天该快递公司的骑手的人均日快递业务量不少于65单的概率;
(Ⅱ)若骑手甲、乙、丙选择了日工资方案(1),丁、戊选择了日工资方案(2).现从上述5名骑手中随机选取2人,求至少有1名骑手选择方案(2)的概率;
(Ⅲ)若仅从人均日收入的角度考虑,请你利用所学的统计学知识为新聘骑手做出日工资方案的选择,并说明理由(同组中的每个数据用该组区间的中点值代替)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冠状病毒是一个大型病毒家族,已知可引起感冒以及中东呼吸综合征![]() 和严重急性呼吸综合征
和严重急性呼吸综合征![]() 等较严重疾病. 而今年出现的新型冠状病毒
等较严重疾病. 而今年出现的新型冠状病毒![]() 是以前从未在人体中发现的冠状病毒新毒株. 人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等. 在较严重病例中感染可导致肺奖、严重急性呼吸综合征、贤衰竭,甚至死亡.核酸检测是诊断新冠肺炎的重要依据,首先取病人的唾液或咽拭子的样本,再提取唾液或咽拭子样本里的遗传物质,如果有病毒,样本检测会呈现阳性,否则为阴性. 根据统计发现,疑似病例核酸检测呈阳性的概率为
是以前从未在人体中发现的冠状病毒新毒株. 人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等. 在较严重病例中感染可导致肺奖、严重急性呼吸综合征、贤衰竭,甚至死亡.核酸检测是诊断新冠肺炎的重要依据,首先取病人的唾液或咽拭子的样本,再提取唾液或咽拭子样本里的遗传物质,如果有病毒,样本检测会呈现阳性,否则为阴性. 根据统计发现,疑似病例核酸检测呈阳性的概率为![]() ,现有
,现有![]() 例疑似病例,分别对其取样、检测,多个样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验,混合样本中只要有病毒,则混合样本化验结果就会呈阳性,若混合样本呈阳性,则将该组中各个样本再逐个化验;若混合样本呈阴性,则该组各个样本均为阴性.现有以下三种方案:
例疑似病例,分别对其取样、检测,多个样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验,混合样本中只要有病毒,则混合样本化验结果就会呈阳性,若混合样本呈阳性,则将该组中各个样本再逐个化验;若混合样本呈阴性,则该组各个样本均为阴性.现有以下三种方案:
方案一:逐个化验;
方案二:四个样本混在一起化验;
方案三: 平均分成两组化验.
在新冠肺炎爆发初期,由于检查能力不足,化检次数的期望值越小,则方案越“优”.
(1)若![]() ,求
,求![]() 个疑似病例样本混合化验结果为阳性的概率;
个疑似病例样本混合化验结果为阳性的概率;
(2)若![]() ,现将该
,现将该![]() 例疑似病例样本进行化验,请问:方案一、二、 三中哪个最“优”?
例疑似病例样本进行化验,请问:方案一、二、 三中哪个最“优”?
(3)若对![]() 例疑似病例样本进行化验,且“方案二”比“方案一”更“优”,求
例疑似病例样本进行化验,且“方案二”比“方案一”更“优”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年末,武汉出现新型冠状病毒(![]() 肺炎疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,目前没有特异治疗方法.防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,某社区将本社区的排查工作人员分为
肺炎疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,目前没有特异治疗方法.防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,某社区将本社区的排查工作人员分为![]() ,
,![]() 两个小组,排查工作期间社区随机抽取了100户已排查户,进行了对排查工作态度是否满意的电话调查,根据调查结果统计后,得到如下
两个小组,排查工作期间社区随机抽取了100户已排查户,进行了对排查工作态度是否满意的电话调查,根据调查结果统计后,得到如下![]() 的列联表.
的列联表.
是否满意 组别 | 不满意 | 满意 | 合计 |
| 16 | 34 | 50 |
| 2 | 45 | 50 |
合计 | 21 | 79 | 100 |
(1)分别估计社区居民对![]() 组、
组、![]() 组两个排查组的工作态度满意的概率;
组两个排查组的工作态度满意的概率;
(2)根据列联表的数据,能否有![]() 的把握认为“对社区排查工作态度满意”与“排查工作组别”有关?
的把握认为“对社区排查工作态度满意”与“排查工作组别”有关?
附表:
|
|
|
|
|
|
|
|
|
|
|
|
附: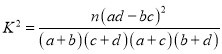
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂制作如图所示的一种标识,在半径为R的圆内做一个关于圆心对称的“H型”图形,“H”型图形由两竖一横三个等宽的矩形组成,两个竖直的矩形全等且它们的长边是横向矩形长边的![]() 倍,设O为圆心,
倍,设O为圆心,![]() ,“H”型图形的面积为S.
,“H”型图形的面积为S.
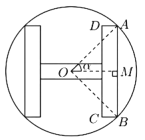
(1)将AB、AD用R、![]() 表示,并将S表示成
表示,并将S表示成![]() 的函数;
的函数;
(2)为了突出“H”型图形,设计时应使S尽可能大,则当![]() 为何值时,S最大?并求出S的最大值.
为何值时,S最大?并求出S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com