
 如图,在六面体ABCD-A1B1C1D1中,平面ABCD∥平面A1B1C1D1,DD1∥平面A1B1BA,DD1∥平面B1BCC1.
如图,在六面体ABCD-A1B1C1D1中,平面ABCD∥平面A1B1C1D1,DD1∥平面A1B1BA,DD1∥平面B1BCC1.分析 (1)利用线面平行的性质可证DD1∥AA1,DD1∥CC1,于是可得AA1∥平面BCC1B1,再利用线面平行的性质得出AA1∥BB1,从而由平行公理可得出DD1∥BB1;
(2)连接AC,BD交点为O,取OB的中点E,设D1B1交MN于F,连接EF,则可证DB⊥平面MNE,于是VD-MNB=VD-MNE+VB-MNE=$\frac{1}{3}$S△MNE•DE+$\frac{1}{3}$S△MNE•BE=$\frac{1}{3}$S△MNE•DB.
解答 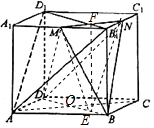 证明:(1)∵DD1∥平面A1B1BA,DD1?平面DD1A1A,平面DD1A1A∩平面A1B1BA=AA1,
证明:(1)∵DD1∥平面A1B1BA,DD1?平面DD1A1A,平面DD1A1A∩平面A1B1BA=AA1,
∴DD1∥AA1.
同理可得DD1∥CC1,
∴AA1∥CC1,又AA1?平面BCC1B1,CC1?平面BCC1B1,
∴AA1∥平面BCC1B1,
又AA1?平面ABB1A1,平面ABB1A1∩平面BCC1B1=BB1,
∴AA1∥BB1,
又DD1∥AA1.
∴DD1∥BB1.
(2)连接AC,BD交点为O,取OB的中点E,设D1B1交MN于F,连接EF,
∵M,N分别是棱A1B1,B1C1的中点,
∴B1F$\stackrel{∥}{=}$BE,
∴BB1∥EF,又BB1⊥平面ABCD,
∴EF⊥平面ABCD,∴EF⊥D1B1,
∵四边形A1B1C1D1是菱形,∴D1B1⊥A1C1,
∴D1B1⊥平面MNE,∴DB⊥平面MNE.
∵六面体ABCD-A1B1C1D1的棱长均为2,BB1⊥平面ABCD,∠BAD=60°,
∴MN=$\frac{1}{2}$AC=$\sqrt{3}$,EF=2,BD=2,
∴VD-MNB=VD-MNE+VB-MNE=$\frac{1}{3}$S△MNE•DE+$\frac{1}{3}$S△MNE•BE=$\frac{1}{3}$S△MNE•DB=$\frac{1}{3}×$$\frac{1}{2}$×$\sqrt{3}×2$×2=$\frac{2\sqrt{3}}{3}$.
点评 本题考查了线面平行的性质,线面垂直的判定,棱锥的体积计算,属于中档题.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:选择题
 如图,在四面体ABCD中,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}=\overrightarrow b,\overrightarrow{AD}$=$\overrightarrow c$,点M在AB上,且AM=$\frac{2}{3}$AB,点N是CD的中点,则$\overrightarrow{MN}$=( )
如图,在四面体ABCD中,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}=\overrightarrow b,\overrightarrow{AD}$=$\overrightarrow c$,点M在AB上,且AM=$\frac{2}{3}$AB,点N是CD的中点,则$\overrightarrow{MN}$=( )| A. | $\frac{1}{2}\overrightarrow a-\frac{2}{3}\overrightarrow b+\frac{1}{2}\overrightarrow c$ | B. | $-\frac{2}{3}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{1}{2}\overrightarrow c$ | C. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b-\frac{1}{2}\overrightarrow c$ | D. | $-\frac{2}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b-\frac{1}{2}\overrightarrow c$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | $\frac{1}{2}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
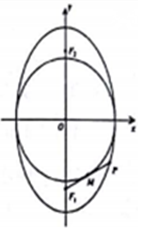 若F1,F2是椭圆C:$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{m}$=1(0<m<9)的两个焦点,椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点M.
若F1,F2是椭圆C:$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{m}$=1(0<m<9)的两个焦点,椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com