
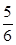 ,
,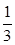
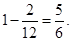 其中甲不在A岗位,乙不在B岗位,丙不在C岗位的情况有4种,所以概率为
其中甲不在A岗位,乙不在B岗位,丙不在C岗位的情况有4种,所以概率为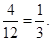


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源:不详 题型:单选题
| A.21 | B.35 | C.42 | D.70 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.56个 | B.57个 | C.58个 | D.60个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.96 | B.48 | C.36 | D.24 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 中,使相邻两数都互质的不同排列方式共有( )种
中,使相邻两数都互质的不同排列方式共有( )种| A.576 | B.720 | C.864 | D.1152 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com