
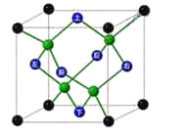
【题目】金刚石是碳原子的一种结构晶体,属于面心立方晶胞(晶胞是构成晶体的最基本的几何单元),即碳原子处在立方体的![]() 个顶点,
个顶点,![]() 个面的中心,此外在立方体的对角线的
个面的中心,此外在立方体的对角线的![]() 处也有
处也有![]() 个碳原子,如图所示(绿色球),碳原子都以共价键结合,原子排列的基本规律是每一个碳原子的周围都有
个碳原子,如图所示(绿色球),碳原子都以共价键结合,原子排列的基本规律是每一个碳原子的周围都有![]() 个按照正四面体分布的碳原子.设金刚石晶胞的棱长为
个按照正四面体分布的碳原子.设金刚石晶胞的棱长为![]() ,则正四面体
,则正四面体![]() 的棱长为__________;正四面体
的棱长为__________;正四面体![]() 的外接球的体积是__________.
的外接球的体积是__________.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,将其左、右焦点和短轴的两个端点顺次连接得到一个面积为
,将其左、右焦点和短轴的两个端点顺次连接得到一个面积为![]() 的正方形.
的正方形.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点(均不在
两点(均不在![]() 轴上),点
轴上),点![]() ,若直线
,若直线![]() 、
、![]() 、
、![]() 的斜率成等比数列,且
的斜率成等比数列,且![]() 的面积为
的面积为![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种电子产品,每件产品合格的概率均为![]() ,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验
,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验![]() 件该产品,且每件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检验方案:将产品每
件该产品,且每件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检验方案:将产品每![]() 个(
个(![]() )一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或
)一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或![]() 次.设该工厂生产
次.设该工厂生产![]() 件该产品,记每件产品的平均检验次数为
件该产品,记每件产品的平均检验次数为![]() .
.
(1)![]() 的分布列及其期望;
的分布列及其期望;
(2)(i)试说明,当![]() 越大时,该方案越合理,即所需平均检验次数越少;
越大时,该方案越合理,即所需平均检验次数越少;
(ii)当![]() 时,求使该方案最合理时
时,求使该方案最合理时![]() 的值及
的值及![]() 件该产品的平均检验次数.
件该产品的平均检验次数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一位发烧病人的体温记录折线图,下列说法不正确的是( )
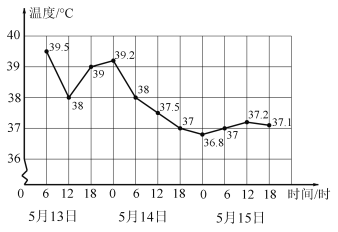
A.病人在5月13日12时的体温是![]()
![]()
B.病人体温在5月14日0时到6时下降最快
C.从体温上看,这个病人的病情在逐渐好转
D.病人体温在5月15日18时开始逐渐稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①函数![]() 的图象把圆
的图象把圆![]() 的面积两等分
的面积两等分
②![]() 是周期为
是周期为![]() 的函数
的函数
③函数![]() 在区间
在区间![]() 上有3个零点
上有3个零点
④函数![]() 在区间
在区间![]() 上单调递减
上单调递减
其中所有正确结论的编号是( )
A.①③④B.②④C.①④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在![]() 上任意一点
上任意一点![]() 处的切线
处的切线![]() 为
为![]() ,若过右焦点
,若过右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,已知在点
两点,已知在点![]() 处切线相交于
处切线相交于![]() .
.
(Ⅰ)求![]() 点的轨迹方程;
点的轨迹方程;
(Ⅱ)①若过点![]() 且与直线
且与直线![]() 垂直的直线(斜率存在且不为零)交椭圆
垂直的直线(斜率存在且不为零)交椭圆![]() 于
于![]() 两点,证明
两点,证明![]() 为定值.
为定值.
②四边形![]() 的面积是否有最小值,若有请求出最小值;若没有请说明理由.
的面积是否有最小值,若有请求出最小值;若没有请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(1)若厂家库房中(视为数量足够多)的每件产品合格的概率为 ![]() 从中任意取出 3件进行检验,求至少有
从中任意取出 3件进行检验,求至少有![]() 件是合格品的概率;
件是合格品的概率;
(2)若厂家发给商家![]() 件产品,其中有
件产品,其中有![]() 不合格,按合同规定 商家从这
不合格,按合同规定 商家从这![]() 件产品中任取
件产品中任取![]() 件,都进行检验,只有
件,都进行检验,只有![]() 件都合格时才接收这批产品,否则拒收.求该商家可能检验出的不合格产品的件数ξ的分布列,并求该商家拒收这批产品的概率.
件都合格时才接收这批产品,否则拒收.求该商家可能检验出的不合格产品的件数ξ的分布列,并求该商家拒收这批产品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,直线![]() 将矩形纸
将矩形纸![]() 分为两个直角梯形
分为两个直角梯形![]() 和
和![]() ,将梯形
,将梯形![]() 沿边
沿边![]() 翻折,如图2,在翻折的过程中(平面
翻折,如图2,在翻折的过程中(平面![]() 和平面
和平面![]() 不重合),下面说法正确的是
不重合),下面说法正确的是
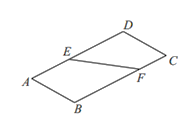
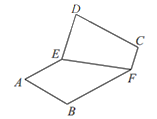
图1 图2
A.存在某一位置,使得![]() 平面
平面![]()
B.存在某一位置,使得![]() 平面
平面![]()
C.在翻折的过程中,![]() 平面
平面![]() 恒成立
恒成立
D.在翻折的过程中,![]() 平面
平面![]() 恒成立
恒成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地为鼓励群众参与“全民读书活动”,增加参与读书的趣味性.主办方设计这样一个小游戏:参与者抛掷一枚质地均匀的骰子(正方体,六个面上分别标注1,2,3,4,5,6六个数字).若朝上的点数为偶数.则继续抛掷一次.若朝上的点数为奇数,则停止游戏,照这样的规则进行,最多允许抛掷3次.每位参与者只能参加一次游戏.
(1)求游戏结束时朝上点数之和为5的概率;
(2)参与者可以选择两种方案:方案一:游戏结束时,若朝上的点数之和为偶数,奖励3本不同的畅销书;若朝上的点数之和为奇数,奖励1本畅销书.方案二:游戏结束时,最后一次朝上的点数为偶数,奖励5本不同的畅销书,否则,无奖励.试分析哪一种方案能使游戏参与者获得更多畅销书奖励?并说明判断的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com