
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
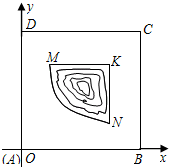 (2011•徐州模拟)如图,某新建小区有一片边长为1(单位:百米)的正方形剩余地块ABCD,中间部分MNK是一片池塘,池塘的边缘曲线段MN为函数y=
(2011•徐州模拟)如图,某新建小区有一片边长为1(单位:百米)的正方形剩余地块ABCD,中间部分MNK是一片池塘,池塘的边缘曲线段MN为函数y=| 2 |
| 9x |
| 1 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 | x |
查看答案和解析>>
科目:高中数学 来源:2011年江苏省徐州市高三第三次质量检测数学试卷(解析版) 题型:解答题

 的图象,另外的边缘是平行于正方形两边的直线段.为了美化该地块,计划修一条穿越该地块的直路(宽度不计),直路l与曲线段MN相切(切点记为P),并把该地块分为两部分.记点P到边AD距离为t,f(t)表示该地块在直路左下部分的面积.
的图象,另外的边缘是平行于正方形两边的直线段.为了美化该地块,计划修一条穿越该地块的直路(宽度不计),直路l与曲线段MN相切(切点记为P),并把该地块分为两部分.记点P到边AD距离为t,f(t)表示该地块在直路左下部分的面积.
查看答案和解析>>
科目:高中数学 来源:2012年福建省莆田市高中毕业班教学质量检查数学试卷(理科)(解析版) 题型:解答题
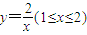 的图象.为了便于游客观光,拟在观光区内铺设一条穿越该区域的直路l(宽度不计),其与人工湖左下方曲线段MN相切(切点记为P),并把该区域分为两部分.现直路l左下部分区域规划为花圃,记点P到边AD距离为t,f(t)表示花圃的面积.
的图象.为了便于游客观光,拟在观光区内铺设一条穿越该区域的直路l(宽度不计),其与人工湖左下方曲线段MN相切(切点记为P),并把该区域分为两部分.现直路l左下部分区域规划为花圃,记点P到边AD距离为t,f(t)表示花圃的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com