
����Ŀ������ ��ͼ�����Ϊ��������
��ͼ�����Ϊ��������
A.  B.
B. 
C.  D.
D. 
���𰸡�C
��������
�ɺ����Ľ���ʽ ����![]() ʱ,�Ǻ�����һ�����,�����ų�A,B,
ʱ,�Ǻ�����һ�����,�����ų�A,B,
��x��(0,1)ʱ��cosx>0��![]() ,����f(x) <0��������ͼ����x���·����ų�D.
,����f(x) <0��������ͼ����x���·����ų�D.
����ѡ��Cѡ��.
�㾦������ͼ���ʶ��ɴ����·������֣�(1)�Ӻ����Ķ������ж�ͼ�������λ�ã��Ӻ�����ֵ���ж�ͼ�������λ�ã�(2)�Ӻ����ĵ����ԣ��ж�ͼ��ı仯���ƣ�(3)�Ӻ�������ż�ԣ��ж�ͼ��ĶԳ��ԣ�(4)�Ӻ����������㣬�ų�����Ҫ���ͼ���������������ų���ɸѡѡ�
�����͡���ѡ��
��������
12
����Ŀ����![]() ����
����![]() ����Сֵ�ǣ�������
����Сֵ�ǣ�������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������̨ABCD��A1B1C1D1�У�AA1�͵���ABCD���ı���ABCDΪ���Σ���BAD=120�㣬AB=AA1=2A1B1=2�� ������MΪCD�е㣬��֤��AM��ƽ��AA1B1B��
������ֱ��DD1��ƽ��A1BD���ɽǵ�����ֵ��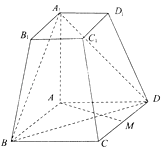
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪Բ![]() ��
��![]() ������ҽ���ֱ�Ϊ
������ҽ���ֱ�Ϊ![]() ����
����![]() ��������Ľ���Ϊ
��������Ľ���Ϊ![]() .
.
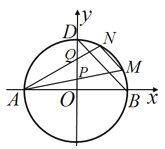
��1����ֱ��![]() ����
����![]() ������Բ
������Բ![]() ���У���ֱ��
���У���ֱ��![]() �ķ��̣�
�ķ��̣�
��2������![]() ��Բ
��Բ![]() �ϵ�һ�����ڵĵ㣬ֱ��
�ϵ�һ�����ڵĵ㣬ֱ��![]() �ֱ���
�ֱ���![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ���߶�
���߶�![]() ���е㣬ֱ��
���е㣬ֱ��![]() ����ֱ��
����ֱ��![]() ��б��.
���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��AB�ǡ�O��ֱ����VA ��ֱ�ڡ�O���ڵ�ƽ�棬��C��Բ���ϲ�ͬ��A��B������һ�㣬M��N�ֱ�ΪVA��VC���е㣬�����н�����ȷ����( ��)

A. MN��AB B. MN��BC���ɵĽ�Ϊ45��
C. OC��ƽ��VAC D. ƽ��VAC��ƽ��VBC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f(x)=|x+a|+|2x+1|,a��R.
(1)��a=1ʱ����ʽf(x)��1�Ľ⼯��
(2)�����x�IJ���ʽf(x)��-2x+1�Ľ⼯ΪP����![]() P����a��ȡֵ��Χ.
P����a��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() +
+ ![]() =1��a��b��0�������ҽ���ֱ�ΪF1��F2 �� ��ԲC����P��1��
=1��a��b��0�������ҽ���ֱ�ΪF1��F2 �� ��ԲC����P��1�� ![]() ����ֱ��PF1��y����Q����
����ֱ��PF1��y����Q���� ![]() =2
=2 ![]() ��OΪ����ԭ�㣮
��OΪ����ԭ�㣮
��1������ԲC�ķ��̣�
��2����M����ԲC���϶��㣬����M�ֱ���ֱ��MA��MB����ԲC��A��B���㣬��������ֱ�ߵ�б�ʷֱ�Ϊk1 �� k2 �� ��k1+k2=2��֤����ֱ��AB�����㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��1��2��������P��5����2����ֱ����������y2=4x�ཻ��B��C���㣬���ABC�ǣ� ��
A.ֱ��������
B.�۽�������
C.���������
D.����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��ͼ�����ɺ���
��ͼ�����ɺ���![]() ��ͼ�����±任�õ����Ƚ�
��ͼ�����±任�õ����Ƚ�![]() ͼ�������е���������쳤��ԭ����2���������겻�������ٽ����õ���ͼ������ƽ��
ͼ�������е���������쳤��ԭ����2���������겻�������ٽ����õ���ͼ������ƽ��![]() ����λ����.
�������.
����������![]() �Ľ���ʽ��������ͼ��ĶԳ��᷽�̣�
�Ľ���ʽ��������ͼ��ĶԳ��᷽�̣�
��������֪����![]() �ķ���
�ķ���![]() ��
��![]() ����������ͬ�Ľ�
����������ͬ�Ľ�![]() ��
��
��1����ʵ��m��ȡֵ��Χ��
��2��֤����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������жϴ������
A. ���������![]() ������̬�ֲ�
������̬�ֲ�![]() ,��
,��![]() ��
��
B. ��![]() ������
������![]() ��ɢ�㶼��
��ɢ�㶼��![]() �ϣ������ϵ��
�ϣ������ϵ��![]() ��
��
C. ���������![]() ���Ӷ���ֲ���
���Ӷ���ֲ��� ![]() , ��
, ��![]() ��
��
D. ![]() ��
��![]() �ij�ֲ���Ҫ������
�ij�ֲ���Ҫ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com