Question

若三条直线x+y+1=0，2x-y+8=0和ax+3y-5=0共有三个不同的交点，则实数a满足的条件是    ．

Answer 1

【答案】分析：由题意知，三直线不共点，前两直线的交点（-3，2）不在ax+3y-5=0上，-3a+6-5≠0．
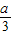
而且任意两直线不平行，∴-1≠-，且 2=-，从而得到实数a满足的条件．
解答：解：由题意得直线x+y+1=0与 2x-y+8=0 的交点（-3，2）不在ax+3y-5=0上，∴-3a+6-5≠0，
a≠．
而且，任意两直线不平行，∴-1≠-，且 2≠-，∴a≠3，且 a≠-6，
故答案为：．
点评：本题考查两直线的位置关系，判断三直线不共点，而且任意两直线不平行是解题的关键，体现了分类讨论的数学思想．